The pyramid data structure,
cxPyramid, defines the relationship between the
different layers of data required to build a pyramidal structure. In finite
element data, you can consider the element grid as a collection of vertices
(points), edges (lines), faces (polygons), elements (three-dimensional
cells), objects (collections of 3-D elements), assemblies (collections of
objects), and so on. You can fit these together to make an object from faces,
bounded by edges, which are in turn delimited by vertices.
Because
cxPyramid
combines several data types, it is an extremely flexible and powerful
structure; witness its ability to handle both finite element data and
molecular data. The flexibility of the
cxPyramid
data type also makes it somewhat difficult to use properly. It may take a
little practice before the method of creating pyramids out of an hierarchical
collection of points, lines, polygons, and elements makes sense.
In many cases where you are representing finite element data, it is
simplest to use the
pyramid dictionary
representation. The reason is that the dictionary elements already contain
the detailed hierarchy of points, lines, and faces. You simply create a list
of vertices making up the overall finite element structure or irregular grid,
and then describe the final structure as a collection of element types, each
of which depends on certain identified vertices. Use of the dictionary also
serves to cut down on the unnecessary repetition of information in the
interests of computational and storage efficiencies.
You can write two kinds of pyramid modules; those that read pyramid data,
such as
ComposePyr, and those that process pyramid data, such as
IsosurfacePyr. It is relatively easy to write a pyramid reader module
without having to be an expert on pyramid structure and the first part of
this chapter explains how to do so, using two code examples. If you want to
write a pyramid processing module, you need to understand the finer details
of pyramid composition, and these are discussed later in the chapter.
The
cxPyramid
data type is a root data type, which means it can be used on module ports to
pass data into and out of modules. A pyramid consists of three main parts:
The structure of
cxLattice
is described in
Chapter
3, "Using the Lattice Data Type".
Pyramid layers and connections are described in detail in
"Pyramid Layer Connections".
This is the data type definition for
cxPyramid:
These are the variables for the pyramid:
A pyramid that incorporates a pyramid dictionary is said to be a
compressed pyramid
as opposed to the
uncompressed pyramids
lacking such a dictionary. A
pyramid dictionary
is simply a collection of uncompressed pyramids that describe in full detail
their reference elements.
You can use pyramid dictionaries to:
The
cxPyramidReference
data structure, described in
"Structure of a Dictionary", lets you specify the
composition of your pyramid in terms of already-defined pyramidal elements.
For example, to create a tetrahedral finite element grid, you would specify
the element type as tetrahedral, list the vertices necessary to create the
grid, and enumerate the constituent tetrahedra based on their four corner
vertices.
For a grid of hexahedral bricks, you would specify the type as hexahedral,
list the vertices necessary to create the grid, and enumerate the constituent
hexahedral bricks based on their eight corner vertices. This is illustrated
in the
SimplePyrReader
module described below.
The best way to learn how to use the pyramid data type is by example. The
next section provides two examples of user functions for pyramid modules.
This example, called
SimplePyrReader, takes in nodal points, reads them and makes
hexahedrons from them. It is a good template for creating any pyramid reader
module that deals with only one data type. It uses compression and refers to
the default pyramid dictionary. Note: As mentioned above, this reader module will only
create a single type of pyramid. It is presented here for reasons
of simplicity. The more general ReadPyr module creates any
type of pyramid and supports a richer input file format. Files
written in this `plain' ASCII format can be immediately read by
ReadPyr. The ReadPyr help page
contains details of the plain ASCII pyramid format.
Alternatively, see the file
$EXPLORERHOME/data/pyramid/README.PlainFormat. Example
data files in the plain format may be found in the same
directory. The C source code for SimplePyrReader is in
$EXPLORERHOME/src/MWGcode/Pyramid/C/reader.c
and the Fortran source is in
$EXPLORERHOME/src/MWGcode/Pyramid/Fortran/reader.f.
The directories also contain copies of an example input data file,
sample.data
(see below), and an example map
SamplePyrReader.map. You can test the module by building it,
loading the example map into the Map Editor, and viewing the points,
vectors and polygons in the pyramid.
This is the
sample.data
file, which contains toy finite element data. The reading of this file (see
the source code below) allows for blank lines, but no other text (such as
comments, for example).
The first line gives the number of nodes (12), the number of data
variables (1) and the number of hexahedrons or bricks (2). The next 12 lines
list the coordinates (x,y,z) and the data value for each node. The data
variable is pressure, changing in the Z direction. The bricks have eight
nodes each, but share one face (four nodes) so there is a total of 12 nodes.
The last two lines define the connectivity list, or the relationship
between the nodes that make up the bricks. The two bricks share the face
delineated by nodes 4, 5, 6, and 7. The nodes are connected in the sequence
indicated in the first list; the first brick is defined in the penultimate
line, and the second brick is defined in the final line. The form of the
hexahedron in the default pyramid dictionary is shown in
Figure
4-1.
This is the user function for
SimplePyrReader.
If you want to build a pyramid reader module that can handle several data
types, use the source code for
ComposePyr
as a template. It references the complete pyramid dictionary. The source code
is in
$EXPLORERHOME/src/ComposePyr/compose.c.
The dictionary reference elements serve as building blocks from which the
final pyramid is constructed. They include 2-D elements, such as triangles
and quadrilaterals, and 3-D elements, such as hexahedrons (or bricks) and
tetrahedrons. The IRIS Explorer default dictionary contains some of the most
commonly used reference elements (see
Figure
4-1).
The vertices are labelled in the order that IRIS Explorer requires to make
each form, counter-clockwise on the bottom and then counter- clockwise on the
top. You provide this information in the
Note: The vertex labelling of these elements is critical. The
sequence determines how the vertices you provide in the connection list are
interpreted. If you label the vertices differently, your finite element mesh
will be made up of distorted or inverted elements.
Table
4-1
lists the elements illustrated above, with the dictionary name and number of
nodes that make up each element.
Note: cx_pyramid_dict_brick
and
cx_pyramid_dict_hexahedron
are synonyms; they can be used interchangably.
This pyramid type is useful for storing the results of finite
element-based simulations. It consists of several levels: the base lattice
and a number of layers, each of which contains a lattice with data and
coordinates, if needed, and the connections between layers. The number of
layers in a pyramid is infinite in theory, although in practice, pyramids
tend to be self-limiting. A pyramid usually has at least three levels,
including a base lattice.
The structure of the finite element pyramid requires that the lattice at
each level
must
be a 1-D curvilinear lattice. The 1-D restriction is so that the indexing
information in the connections list makes sense. But there is a natural
ordering from the nodes in a 3-D lattice to nodes in a 1-D lattice, so you
can break out data from a 3-D lattice fairly easily into a 1-D lattice for
inclusion in a pyramid. The natural ordering, or memory layout, of data in
two or more dimensions gives the usual 1-D indexing into the array.
Figure
4-2
shows a 2-D lattice that, when translated into a 1-D curvilinear lattice
(for inclusion in a pyramid layer, say) has 35 nodes, indexed as 0-34.
Note: In this figure, we have assumed the data is laid out in the
C language (row-major) convention (see
Figure
3-4).
Not all lattices in a pyramid need have data or coordinates. The base
lattice, which contains all the nodal data and coordinate values, is
frequently the only lattice that contains coordinate information at all. The
0-layer lattice can store edge-based data, and the 1-layer lattice can
contain face-centered data, such as the mass flux, for example. The 2-layer
lattice can store volumetric or centroid data, such as a mass fraction,
centroid pressure, or gauss point information. In addition, the lattice at
each layer can store the physical location of each piece of data in its
coordinates part. For example, the mass flux through a face could be
assigned to the coordinates of the midpoint of the face, or some other
location on the face. Similarly, cell-based data such as pressure or
composition could be explicitly associated with a position within the cell
(at, say, its center, or some other point). See
The Pyramid Layers
below for more about the way in which the lattice is defined within the
layer.
The
ClipPyr
and
CropPyr
modules work by removing elements at the highest level in the pyramid, if
those elements contain any vertices outside the bounding plane(s). Therefore,
you should construct finite element meshes with the top level being the most
natural component. Often, this will mean that a finite element mesh has three
layers in the pyramid (i.e.
The pyramid structure is built from lattices layered onto the base
lattice.
Figure
4-3
shows the relationship between elements and layers in an uncompressed
tetrahedral pyramid. It illustrates how a finite element grid can be built
from the hierarchy of relationships between four vertices.
However, the simplest tetrahedral grid is just an array of tetrahedra,
defined by specifying their vertices. The vertex locations and data are
stored in the base lattice. You can omit edge and face information and go
directly to the 3-D element layer of the pyramid. The
cxConnection
structure of this layer (layer[2]
in C or
layer(3)
in Fortran) really does all the work of constructing the tetrahedral grid.
The example in
Figure
4-3
is made up of 32 tetrahedra, and so we can start to set values for some of
the members of the
cxConnection
component of the layer:
Here,
numElements
is the number of
elements
(i.e., tetrahedra in the current example) in this layer, while
elements
is an array of length
elemArrayLen
which contains the indices into the
connections
array (see below) for each element in this layer.
The vertices are labelled in the order shown in
Figure
4-4. Grid A shows the vertices at the bottom of the structure and grid B
shows those at the top. Grid C shows the top partially overlaid on the bottom
to illustrate how the tetrahedra are formed.
The connections array is the concatenation of the sets of four vertices
for the 32 tetrahedra:
The construction of the tetrahedra in the example of
Figure 4-4 has been done directly
in terms of their vertices (rather than their faces, edges and vertices), which,
in the discussion above, are the elements in the layer "beneath"
layer[2], which defines the 3-D elements of the
pyramid. We have been able to bypass the intervening layers (which
would ordinarily contain
face and edge connectivity information) because we are using a
compressed
pyramid - i.e. one which contains a pyramid dictionary.
This is described in more detail in the following section.
However, you must still define the lattice and connection list
pairs in the layer[] array above the
compression dimension (see the definition of
nDim in "Structure
of a Dictionary", below).
But below the compression dimension In addition to the omission of some layers, there is an
important change in the cxConnection structure at the
compression layer. At layer[nDim-1] (in C)
or layer(nDim) (in Fortran), the
cxConnection structure must
describe the composition of the compressed elements in terms of their
vertices. You create such a connection list by listing the actual vertex
indices of the baseLattice vertices you wish to go into
the construction of each element, as in the example in "Creating a Tetrahedral Grid".
The integer value that identifies the type of an element is
really just an index into the pyramid dictionary. Since the dictionary is
merely an array of uncompressed pyramids, it is natural to use the array
index of the dictionary element as the identifying value.
In the case of a grid of a single element type, however, the
vector of identical indices is omitted in favor of a single universal
element type. See "Structure of a
Dictionary" below for how to specify these different cases.
Figure 4-5
shows how the tetrahedral grid looks in compressed form.
Figure 4-3
shows the same grid in uncompressed form, with all the layers
visible.
To use a compressed pyramid in this context, you must create your own
data structure showing connectivity between the compressed elements of the
pyramid. See Chapter 8, "Creating User-defined Data
Types" for more information.
If you do not want to use the dictionary, you can represent an
empty dictionary by setting the cxPyramidReference
member compressType to
cx_compress_none. In this case,
cxPyramidDictionary is never referenced.
The brick or hexahedron element, for example, comprises six
faces, each of
which comprises four out of the twelve edges found in the brick. Each of
the twelve edges refers to two endpoint vertices. In the pyramid
dictionary, the vertices are not given data or coordinates because they
are generic elements, without location in Cartesian space or data
values.
This is the type definition for the dictionary data type,
cxPyramidDictionary:
These are the variables:
For
This is the type definition for the dictionary reference structure,
cxPyramidReference:
These are the variables:
A
compressType
value of
cx_compress_unique
indicates that a dictionary is used, but that the current finite element mesh
is composed of only a single reference element type.
A
compressType
value of
cx_compress_multiple
indicates that a dictionary is used and that the current finite element mesh
is composed of one or more reference element types. In this case, each
element at layer
Note: There is no case statement in the
switch (compressType)
for
cx_compress_none, because the case would have no members (since there
is no compression) and this is prohibited by the IRIS Explorer data typing
language. Hence, it doesn't appear in the data type definition. Similarly,
it is absent from the data type
declaration
as well (see
"Data Type Declaration", below).
You use the connection list in each layer of a pyramid to define how
elements in that layer and the one immediately below it are related. For
example, the connection list in layer 0 of a tetrahedron represents the set
of connections between the edge elements in layer 0 and the nodes, or point
elements, in the base lattice. Each line element, or edge, is connected to
two nodes, or vertices, and the concatenation of all connections is
represented by a pair of arrays,
The pyramid layers are described by the
cxPyramidLayer
structure. This is the type definition for a single pyramid layer:
These are the variables:
For more on curvilinear lattices, see
"Curvilinear Lattices".
The connections among elements within a layer can be fairly complex and
each one must be specifically defined in the
cxConnection
structure. This is the type definition for the set of connections in a
pyramid layer:
These are the variables:
Use of these variables is illustrated in
"Creating a Connection List", below.
Figure
4-6
illustrates the components of a connection list for layer 0 of a
tetrahedron. It contains six edge elements connected to four nodes in the
base lattice by twelve dependencies. The connection data structure defines
each edge-vertex relationship specifically (see
"The Pyramid Connections").
You can see how the vertex information and the description of the
connections between them at each level are used to construct 2-D and 3-D
elements, resulting in the creation of a tetrahedron. It is, however, legal
to create a finite element pyramid without base data, coordinates, or indeed
a base lattice at all.
This example shows how you fill out the connections list for each layer in
a pyramid. The data are for the connections illustrated in
Figure
4-6.
- Element 0 has two nodes and points to nodes 0 and 1.
- Element 1 has two nodes and points to nodes 1 and 2.
- Element 2 has two nodes and points to nodes 2 and 0.
- Element 3 has two nodes and points to nodes 0 and 3.
- Element 4 has two nodes and points to nodes 1 and 3.
- Element 5 has two nodes and points to nodes 2 and 3.
It is somewhat involved to write a module that takes a pyramid as input in
order to perform a computation, create a filtered output pyramid, or to
generate geometry for visualization in the
Render
module. You must take into account the hierarchical nature of the pyramid
data, with the added option of a dictionary to indicate element types.
Because a few concepts usually suffice to create a compressed pyramid
manipulation module, the steps to create such a module are given here in
outline form.
The first step is to discover the natural dimension at which the module
works. For example, an isosurface module typically works with a 3-D input in
order to create the isosurface through a single cell. If the input is viewed
as a collection of 3-D cells, the output is a collection of 2-D surfaces. The
behavior of the module is characterized by the dimensionality of input that
it naturally processes. Generally, the input must have at least this
dimensionality (you cannot isosurface a 2-D input and get many useful
results), which translates into a requirement for at least this number of
layers in its pyramid.
The second step is to develop the computational algorithm for the module
assuming the presence of data at the desired level. If the module requires
the full hierarchical information of vertices, edges, and faces, this is the
place to take advantage of it; however, if the module can work by omitting
some layers of data (for instance, by dealing with a face as a list of
vertices) then you should assume that those layers are omitted and that the
pyramid is compressed at the operational layer.
Next, assuming that the pyramid is compressed at the operational layer, or
not at all, loop over all "active" elements. The active elements are those
that are subordinate to some element at the top layer of the pyramid and are
thus reachable from the top. Two API routines exist to list the active
elements at a given layer:
If the pyramid is not compressed, but you wish to deal with compressed
elements, you can create a default dictionary using
Using
At this point you have a module that will work with compressed or expanded
inputs, assuming compression only at the operational layer. Now you must
extend your module to handle inputs that are compressed at the wrong layer.
It is often sufficient to handle inputs that are compressed at too low a
layer by simply expanding them, then dealing with the fully expanded input as
above. The savings due to compression increase with the dimensionality of the
compression (or conversely, decrease with decreasing dimensionality of
compression), so a pyramid that has too low a compression level may not save
much storage. If the cost of expanding an input is likely to prove too great,
then you must extend your computational algorithm to handle compression at
too low a level.
Handling pyramid compression at too high a level is relatively easy, but
requires a little study to master the details. The concept is to represent
each pyramid dictionary reference element at the too-high level as a
collection of known dictionary reference elements at the operational layer,
and then to process the input by processing the equivalent known elements.
Assume that you are writing the 2-D part of
PyrToGeom, which creates shaded polygons from an input pyramid.
However, the input pyramid is compressed at the 3-D cell level. It is
prohibitively expensive in time and memory to expand the pyramid and then
recompress it to faces, so instead you preprocess the 3-D element dictionary
in terms of its faces, then simply draw the faces for each 3-D element.
The first step is to preprocess the pyramid dictionary. The routine
This violates the usual standard that a pyramid dictionary is made up of
fully expanded pyramids, but the violation is temporary, as this output
dictionary is really used as a translation table to process elements at the
operational level.
Figure
4-7
shows the process.
Each of the compressed reference elements now refers to the same
dictionary, which has dimension equal to the operational level. This means
that each reference element is now described in terms of elements that your
algorithm can handle. Furthermore, all the reference elements in the input
dictionary are described in terms of the same dictionary, which you can
include in your output if necessary.
Relating this to the
PyrToGeom
example, you receive a grid of 3-D elements but want to work with faces. So
you call
Now it is easy to process the too highly compressed input. Simply operate
on each active element at the compression level, looking up the element in
the translation dictionary.
The element will comprise one or more elements at the correct level of
compression, which can be processed directly by your algorithm. For instance,
a 3-D prism cell input is made up of triangular and rectangular faces, which
PyrToGeom
can handle.
Lastly, keep track of the vertices that are used to represent each
element. In the original input, the vertices are listed at the compression
layer in the
connections[]
array of the
cxConnection
structure. The input dictionary uses vertices numbered 0, 1, ...
N-1 to indicate the first
N
vertices of the compressed element. During recompression of the input
dictionary, the higher level element is decomposed into lower level elements,
and the relevant vertices from the set [0, 1, ...,
N-1] are used.
It is important to pick up the indirect indexing from both the compressed
dictionary and the input connection list, so that the correct vertices are
used. For example, the prism has six vertices. If vertices 1, 2, 3, 6, 7 and
8 make up a sample prism, then the prism element in the input dictionary
refers to vertices 0-5, meaning the first six vertices of the input element.
Now, if you work with vertices 0, 1, 2, 3, 4 and 5, you will be interpreting
the input data incorrectly. Instead, use the indirect addressing to pick up
0==>1, 1==>2, 2==>3, 3==>6, 4==>7, 5==>8.
The prism will then be made up of faces of two types, triangles (0,1,2)
and rectangles (0,1,2,3). A sample
connection
array for a prism is [ 0 1 2 0 1 4 3 1 2 5 4 2 0 3 5 3 4 5 ]. When you work
with the last triangle in the prism, make sure to index from its vertex
number (0,1,2) into the connection array to get (3,4,5) as the vertices to
look up in the original compressed input, yielding actual vertex numbers
6,7,8. This double translation may seem complex, but it naturally reflects
the compression in two stages, first to too high a level, then down to the
correct level.
Correct application of this technique makes it almost as easy to handle
pyramid compression at any level as it is to handle it only at the desired
level. Source code for the modules
ComposePyr,
CropPyr, and
LatToPyr
is provided in the directories below
$EXPLORERHOME/src.
Most modules operate at a single level, but some, like
PyrToGeom, can operate at many levels. In this case, you can create a
table of operational level versus level of compression. You will usually find
that the table breaks down into actions at the operational level, actions
below that level (including, perhaps, simply expanding the input data), and
recompressing the input dictionary for inputs above the operational level.
Chemistry pyramids are used to construct objects according to information
pertaining to molecular structures. The pyramid structure is more narrowly
defined than that of the finite element pyramid and differs from it as
follows:
The chemistry pyramid has four levels, which are:
Source code examples, in the form of the source code used to build the
modules
MoleculeBuilder
and
ReadPDB, are provided in the directories below
$EXPLORERHOME/src.
Table
4-2
lists the minimum required set of data values for the base lattice and the
layer 0 lattice in a chemistry pyramid.
The connection list from atoms to bonds shows which bonds relate to which
atoms, and the bond lattice's atomic IDs define which atoms are connected by
which bonds. You can supply more information in additional vector components
if you choose.
The
cxPyramid
data type, though defined in the IRIS Explorer typing language, can be
considered as a C structure. Fortran users need to set pointers to the data
type structures when they use them. The type declaration resides in the
header file
$EXPLORERHOME/include/cx/cxPyramid.h.
This is the data type declaration for
cxPyramid:
The case of
cx_compress_none
does not appear in the union because it is empty. It is illegal to use an
empty case in the IRIS Explorer data typing language.
The Fortran type enumerations reside in the file
$EXPLORERHOME/include/cx/cxPyramid.inc.
The compression types are specified by this enumeration:
You can use the API (Application Programming Interface) routines to
manipulate data types in IRIS Explorer. The subroutines for creating and
manipulating pyramids in IRIS Explorer, and for creating and referencing a
pyramid dictionary, are listed below and described in detail in the
IRIS Explorer Reference
Pages or the on-line man pages
The subroutines let you:
Pyramid allocation is based on the number of levels of the pyramid; the
user must allocate the lattice and connections for each level (use
Note: All the subroutines use zero-based indexing except
Table
4-3
lists the pyramid subroutines.
Table
4-4
lists the pyramid dictionary subroutines.
Here are some examples of user functions for pyramid modules.
This example uses compressed pyramids to generate a pyramid. The base
lattice is passed into the module via its input port, and it reads the
pyramid information from an input file. The C source code is in
$EXPLORERHOME/src/MWGcode/Pyramid/C/GeneratePyr.c
and the Fortran source is in
$EXPLORERHOME/src/MWGcode/Pyramid/Fortran/GeneratePyr.f. The
directories also contain copies of an example input data file,
pyr.dat
(see below), and an example map
GeneratePyr.map. You can test the module by building it, loading the
example map into the Map Editor, and viewing the vectors in the pyramid,
then by changing the map and data files (see below).
This is the
pyr.dat
file, which contains information about the pyramid to be generated. The
reading of this file (see the source code below) allows for blank lines, but
no other text (such as comments, for example).
The format of this file is the number of nodes (vertices) in the first
element, followed by a list of the vertices in the first element, followed
by the number of nodes in the second element, etc. The data values and
coordinates of the vertices are taken from the base lattice; the numbering of
the vertices is the same as that of the nodes in the lattice. There is a
direct equivalence between this numbering and that for the connections. In
this example, it can be seen that the pyramid is made up of a prism element,
a tetrahedron element and a brick element.
The example
GeneratePyr.map
uses
GenLat
as the source of the base lattice. As an alternative, you could try reading
this in from a file. For example, here is a file containing coordinates and
data for a set of vertices:
You can read this file using the
ReadXYZData
module, which outputs a 1-D curvilinear lattice. Using this module, the
first three values on each line (apart from the first) are read as the
(x,
y,
z) coordinates of the node, and the fourth value is read as the data
value at that node. Connect its output to the
BaseLat
input port on
GeneratePyr
(footnote)
(see "Wiring Modules
Together" in the
IRIS Explorer User's Guide). Then pass the following input
file to
GeneratePyr:
In this example, the pyramid is composed of a tetrahedral element, a
hexahedral element and a pyramidal element (this division is reflected by the
breaks in the lattice input file, above).
Source code for the modules
ComposePyr
(which is a more complicated variant on the
GeneratePyr
module above),
CropPyr, and
LatToPyr
is provided in the directories below
$EXPLORERHOME/src. To see how the modules are constructed, open the
modulename.mres
files for these modules in the Module Builder.
The Structure of a Pyramid
root typedef struct cxPyramid {
cxLattice baseLattice "Base Lattice";
long count "Num Levels";
cxPyramidLayer layer[count];
cxPyramidReference ref;
} cxPyramid;
Pyramid Dictionaries
A Pyramid Reader Module
12 1 2
0 0 0 100
0 1 0 100
1 1 0 100
1 0 0 100
0 0 1 200
0 1 1 200
1 1 1 200
1 0 1 200
0 0 2 300
0 1 2 300
1 1 2 300
1 0 2 300
0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 11
C Version:
/*
This module is a prototype reader of finite element data.
It reads in nodal points and then the connectivity for the cells.
This code assumes that only one cell type is used. The user
can alter the two define's for a different cell type.
*/
#include <cx/cxPyramid.h>
#include <cx/Pyramid.h>
#include <cx/cxPyramid.api.h>
#include <cx/DataAccess.h>
#include <cx/DataTypes.h>
#include <sys/types.h>
#include <sys/stat.h>
#include <fcntl.h>
#define NODES 8
#define TYPE cx_pyramid_dict_hexahedron
int memclean(cxPyramid *pyr,
cxErrorCode ec,
cxConnection *conn)
{
/* this routine will clear up memory in case of errors */
if(cxDataAllocErrorGet() || (ec != cx_err_none))
{
cxDataRefDec(pyr);
cxDataRefDec(conn);
return 1;
} else {
return 0;
}
}
void read_brick (char *filename,
cxLattice **base_lat,
cxPyramid ** pyramid )
{
FILE *file;
float *coord, *data;
cxConnection *conn;
cxPyramidDictionary *dict;
cxErrorCode ec = cx_err_none;
long *connec, num_nodes, num_bricks;
long nDataVar,i,j,k, *elem;
if(filename == NULL) return;
if(filename[0] == NULL) return;
if((file = fopen(filename,"r")) == NULL)
{
printf("Cannot open file %s\n",filename);
return;
}
/*
get the header information
Number of Nodes,
Number of Data Properties,
Number of elements
*/
fscanf(file,"%ld %ld %ld",&num_nodes, &nDataVar, &num_bricks);
*base_lat = cxLatNew(1,&num_nodes,nDataVar,cx_prim_float,
3,cx_coord_curvilinear);
if(cxDataAllocErrorGet()) return;
cxLatPtrGet(*base_lat,NULL,(void **)&data,NULL,(void **)&coord);
/*
read in the nodal data. This assumes there are 3 coords
and nDataVar data values for each node.
*/
for(i=0,k=0;i<num_nodes;i++)
{
fscanf(file," %f %f %f",&coord[3*i],&coord[3*i+1],&coord[3*i+2]);
for(j=0;j<nDataVar;j++)
fscanf(file,"%f",&data[k++]);
}
/* build up the pyramid by ignoring the intermediate levels */
*pyramid = cxPyrNew(0);
cxPyrSet(*pyramid,*base_lat);
cxPyrLayerSet(*pyramid,1,NULL,NULL);
cxPyrLayerSet(*pyramid,2,NULL,NULL);
/* set up the connections list */
conn = cxConnNew(num_bricks, num_bricks * NODES);
if(memclean(*pyramid,ec,0))return;
cxConnPtrGet(conn,NULL,NULL,&elem,&connec);
*elem++ = 0;
for(i=0,k=0;i<num_bricks;i++)
{
*elem++ = (i+1) * NODES; /* each has NODES nodes per brick */
for(j=0;j<NODES;j++)
{
fscanf(file,"%ld",&connec[k++]); /* read in nodal list */
}
}
cxPyrLayerSet(*pyramid,3,conn,NULL);
if(memclean(*pyramid,ec,conn))return;
/* make the pyramid dictionary */
dict = cxPyrDictDefault( 3 );
cxPyramidDictionarySet( *pyramid, dict, &ec );
if(memclean(*pyramid,ec,conn))return;
cxPyramidCompressionTypeSet( *pyramid,
cx_compress_unique, &ec );
if(memclean(*pyramid,ec,conn))return;
connec = (long *)cxPyramidCompressionIndexGet(*pyramid,&ec);
if(memclean(*pyramid,ec,conn))return;
*connec = TYPE;
}
Fortran Version:
SUBROUTINE RDBRIK(FILNAM,BASLAT,PYRMID)
C
C This module is a prototype reader of finite element data.
C It reads in nodal points and then the connectivity for the cells.
C This code assumes that only one cell type is used. The user
C can alter the two define's for a different cell type.
C
INCLUDE '/usr/explorer/include/cx/Pyramid.inc'
INCLUDE '/usr/explorer/include/cx/cxPyramid.api.inc'
INCLUDE '/usr/explorer/include/cx/DataAccess.inc'
INCLUDE '/usr/explorer/include/cx/DataTypes.inc'
C
C .. Parameters ..
#if defined(IS_64BIT)
INTEGER*8 NODES
#else
INTEGER NODES
#endif
PARAMETER (NODES=8)
C .. Scalar Arguments ..
#if defined(IS_64BIT)
INTEGER*8 BASLAT, PYRMID, NNODES, NDVAR, I, J, NBRIKS
INTEGER*8 CONN, DICT, EC
INTEGER*8 CONNC(1), ELEM(1)
#else
INTEGER BASLAT, PYRMID, NNODES, NDVAR, I, J, NBRIKS
INTEGER CONN, DICT, EC
INTEGER CONNC(1), ELEM(1)
#endif
CHARACTER*(*) FILNAM
C .. Local Scalars ..
INTEGER IER, IFILE, K
C .. Local Arrays ..
REAL COORD(3,1), DATA(1)
C .. External Functions ..
INTEGER MEMCLN
EXTERNAL CXCONNNEW, CXCONNPTRGET, CXDATAALLOCERRORGET,
* CXLATNEW, CXLATPTRGET,
* CXPYRAMIDCOMPRESSIONINDEXGET, CXPYRDICTDEFAULT,
* CXPYRLAYERSET, CXPYRNEW, CXPYRSET, MEMCLN
C .. External Subroutines ..
EXTERNAL CXPYRAMIDCOMPRESSIONTYPESET,
* CXPYRAMIDDICTIONARYSET
C .. Intrinsic Functions ..
INTRINSIC ICHAR
C .. Pointers to Lattice Structures ..
#ifdef WIN32
POINTER(PDATA,DATA)
POINTER(PCOORD,COORD)
POINTER(PELEM,ELEM)
POINTER(PCONNC,CONNC)
#else
POINTER(PDATA,DATA), (PCOORD,COORD)
POINTER(PELEM,ELEM), (PCONNC,CONNC)
#endif
C .. Executable Statements ..
C
C Get the file name from which to read the data
C
IF (ICHAR(FILNAM(1:1)).EQ.0) RETURN
IFILE = 7
EC = CX_ERR_NONE
OPEN (IFILE,FILE=FILNAM,STATUS='old',IOSTAT=IER)
IF (IER.NE.0) THEN
PRINT *, 'Cannot open file', FILNAM
RETURN
END IF
C
C Get the header information (number of Nodes, number of data
C properties, number of elements)
C
READ (IFILE,FMT=*) NNODES, NDVAR, NBRIKS
BASLAT = CXLATNEW(1,NNODES,NDVAR,CX_PRIM_FLOAT,3,
* CX_COORD_CURVILINEAR)
IF (CXDATAALLOCERRORGET().NE.0) RETURN
IER = CXLATPTRGET(BASLAT,I,PDATA,J,PCOORD)
C
C Read in the nodal data. This assumes there are 3 coords
C and nDataVar data values for each node.
C
DO 20 I = 1, NNODES
READ (IFILE,FMT=*) COORD(1,I), COORD(2,I), COORD(3,I),
* (DATA((I-1)*NDVAR+J),J=1,NDVAR)
20 CONTINUE
C
C Build up the pyramid by ignoring the intermediate levels
C
PYRMID = CXPYRNEW(0)
IER = CXPYRSET(PYRMID,BASLAT)
IER = CXPYRLAYERSET(PYRMID,1,0,0)
IER = CXPYRLAYERSET(PYRMID,2,0,0)
C
C Set up the connections list
C
CONN = CXCONNNEW(NBRIKS,NBRIKS*NODES)
IF (MEMCLN(PYRMID,EC,0).NE.0) RETURN
IER = CXCONNPTRGET(CONN,I,J,PELEM,PCONNC)
ELEM(1) = 0
DO 40 I = 1, NBRIKS
ELEM(I+1) = I*NODES
K = (I-1)*NODES
READ (IFILE,FMT=*) (CONNC(J+K),J=1,NODES)
40 CONTINUE
IER = CXPYRLAYERSET(PYRMID,3,CONN,0)
IF (MEMCLN(PYRMID,EC,CONN).NE.0) RETURN
C
C Make the pyramid dictionary
C
DICT = CXPYRDICTDEFAULT(3)
CALL CXPYRAMIDDICTIONARYSET(PYRMID,DICT,EC)
IF (MEMCLN(PYRMID,EC,CONN).NE.0) RETURN
CALL CXPYRAMIDCOMPRESSIONTYPESET(PYRMID,CX_COMPRESS_UNIQUE,EC)
IF (MEMCLN(PYRMID,EC,CONN).NE.0) RETURN
PCONNC = CXPYRAMIDCOMPRESSIONINDEXGET(PYRMID,EC)
IF (MEMCLN(PYRMID,EC,PCONNC).NE.0) RETURN
CONNC(1) = CX_PYRAMID_DICT_HEXAHEDRON
CLOSE (IFILE)
C
RETURN
END
INTEGER FUNCTION MEMCLN(PYR,EC,CONN)
C
C Clear up memory in case of errors
C
INCLUDE '/usr/explorer/include/cx/DataAccess.inc'
INCLUDE '/usr/explorer/include/cx/Typedefs.inc'
C
C .. Scalar Arguments ..
INTEGER CONN, EC, PYR
C .. External Subroutines ..
EXTERNAL CXDATAREFDEC
C .. External Functions ..
EXTERNAL CXDATAALLOCERRORGET
C .. Executable Statements ..
C
MEMCLN = 0
IF ((CXDATAALLOCERRORGET().NE.0) .OR. (EC.NE.CX_ERR_NONE)) THEN
CALL CXDATAREFDEC(PYR)
MEMCLN = 1
CALL CXDATAREFDEC(CONN)
END IF
C
RETURN
END
Reading Several Data Types
Using the Dictionary Elements
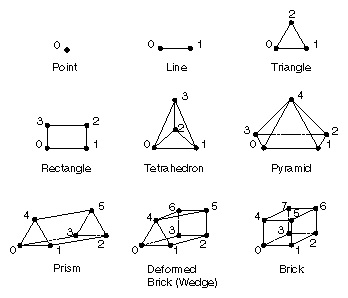
Figure 4-1 Pyramid Dictionary Reference Elements
Dimension
Element
No. of Nodes
Name
0-D
Point
1
cx_pyramid_dict_point
1-D
Line
2
cx_pyramid_dict_line
2-D
Triangle
3
cx_pyramid_dict_triangle
Rectangle
4
cx_pyramid_dict_quadrilateral
3-D
Tetrahedron
4
cx_pyramid_dict_tetrahedron
Pyramid
5
cx_pyramid_dict_pyramid
Prism
6
cx_pyramid_dict_prism
Deformed brick (wedge)
7
cx_pyramid_dict_wedge
Brick (hexahedron)
8
cx_pyramid_dict_brick,
cx_pyramid_dict_hexahedron
Finite Element Pyramids
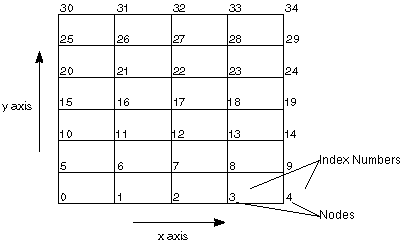
Figure 4-2 Memory Layout of a 2-D Lattice
Contents of Layers
Designing a Finite Element Mesh
Creating a Tetrahedral Grid
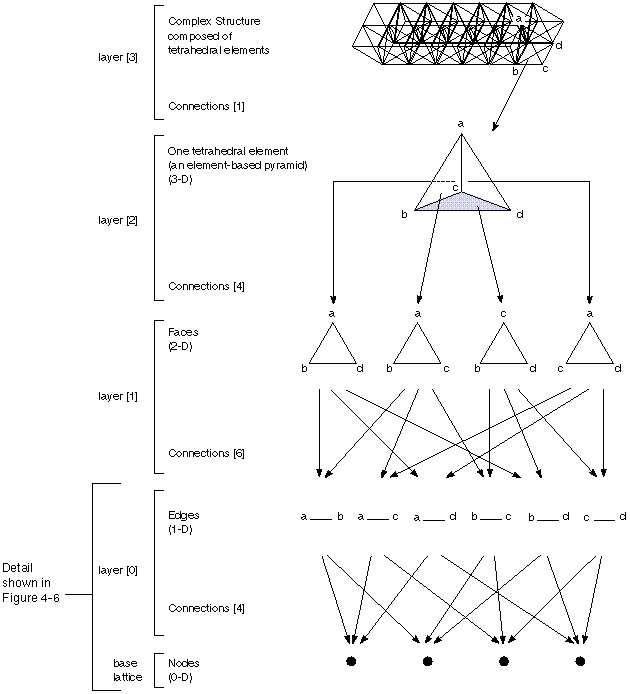
Figure 4-3 Layers in a Tetrahedral Grid
numElements 32
elemArrayLen 33
elements[] 0 4 8 12 16 ... 128
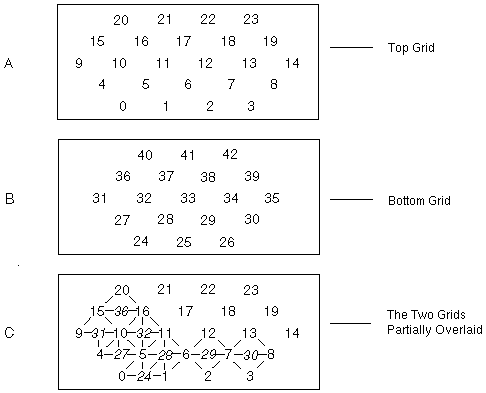
Figure 4-4 Top and Bottom of Compressed Tetrahedral Grid
numConnections 128
connections[] 0 1 5 24
1 2 6 25
2 3 7 26
...
18 23 22 42
where connections is an array of length
numConnections which contains the indices of the elements
in the layer beneath, which are to be connected together to construct the
elements in this layer. The
elements array is used to step along
connections to extract the indices for the
individual elements.
Thus, element number i in this layer is built up by connecting
together elements connections[elements[i]],
connections[elements[i]+1], ...,
connections[elements[i+1]-1] from the layer
beneath this one.
Hence, element number i in this layer is constructed from
connections to N elements from the layer beneath,
where
N = elements[i+1] - elements[i].
See
"Pyramid Layer Connections" for more about the members of
cxConnection.
Using a Pyramid
Dictionary
When you use a pyramid dictionary, some of
the cell structures in the pyramid are compressed and you may
have to enumerate the faces or edges making up the finite element grid. In
general, it is unnecessary to specify any relationship information for the
layers between the vertices and the layer at which dictionary elements are
referenced. It is this careful omission of repetitive data that makes the
pyramid dictionary structure simpler and more compact to use.
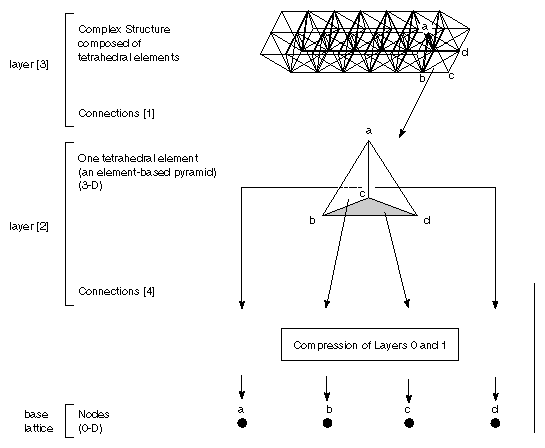
Figure 4-5 Layers in a Compressed Grid
Advantages
Using the
pyramid dictionary has two important advantages. Such a pyramid is easier
to create, because you need only consider the vertices that make up each
element. It also requires much less storage than its fully expanded
version, because each reference element represents the internal
face/edge/vertex hierarchy once for all instances of the type.
Disadvantages
Using
the pyramid dictionary has one drawback, the significance of which depends
on your application. Because the face and edge structure is contained
entirely within the omitted layers of a 3-D compressed pyramid, such a
pyramid has absolutely no representation of the sharing of faces or edges
within the pyramid. An algorithm that requires connectivity information
between cells of a finite element mesh will find such information is not
present in a compressed pyramid.
Structure of a
Dictionary
Each dictionary has a dimensionality, which
is also the dimensionality of all the elements found in it, and a vector
of reference elements described as uncompressed pyramids. The data type
structure is described by cxPyramidDictionary. Figure 4-1 shows the
contents of the default 3-D pyramid dictionary. These nine reference
elements are described as a vector of nine pyramids, each of which
comprises points, lines, and faces for that element.
shared typedef struct {
long nDim "Num Dimensions";
long numEntries "Num Entries";
closed struct cxPyramid table[numEntries] "Table";
} cxPyramidDictionary;
typedef struct {
cxCompressType compressType "Compression Type";
switch (compressType) {
case cx_compress_unique: /* Use one element. */
long index "Compression Index";
case cx_compress_multiple: /* Use many elements. */
long numIndices "Number Indices";
long indices[numIndices] "Compression Index";
} r;
cxPyramidDictionary dictionary "Dictionary";
} cxPyramidReference;
Pyramid Layer Connections
typedef struct {
closed cxConnection relation "Layer %d Connection";
closed cxLattice nextLattice "Layer %d Lattice";
} cxPyramidLayer;
The Pyramid Connections
shared typedef struct {
long numElements "Num Elements";
long elemArrayLen "Elements Array Length";
long numConnections "Connections Array Length";
long elements[elemArrayLen] "Elements Array";
long connections[numConnections] "Connections Array";
} cxConnection;
Connection List Components
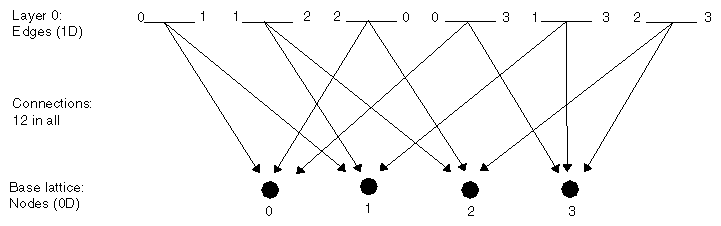
Figure 4-6 Connections in a Tetrahedron
Creating a Connection List
Using the Compressed Pyramid API
Designing a Compressed Pyramid Module
Dealing with Compressed Elements
Handling Compression at Non-operational Levels
A Practical Example
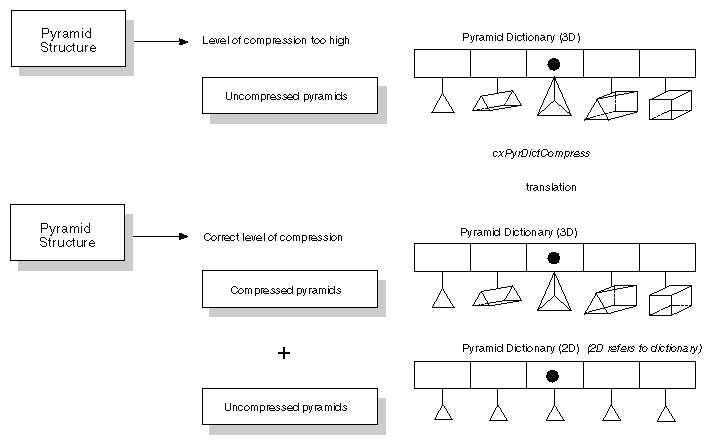
Figure 4-7 Preprocessing a Pyramid Dictionary
Chemistry Pyramids
Base Lattice Values
Layer 0 Lattice Values
Type: 1 = single, 2 = double, 3 = triple, 4 = H-bond, 5 =
aromatic
ID number
First atomic number of the bond
Element number (from the Periodic Table of the Elements)
Second atomic number of the bond
Van der Waals radius
Topology: 1 = in ring, 2 = chain
Color index
Covalent radius
Mass
Charge
Valence
Radical
Ionization
Hybridization
Data Type Declaration
#include <cx/cxLattice.h>
typedef enum {
cx_compress_none,
cx_compress_unique,
cx_compress_multiple
} cxCompressType;
typedef struct cxConnection {
long numElements;
long elemArrayLen;
long numConnections;
long *elements;
long *connections;
} cxConnection;
typedef struct cxPyramidLayer {
cxConnection *relation;
cxLattice *nextLattice;
} cxPyramidLayer;
typedef struct cxPyramidDictionary {
long nDim;
long numEntries;
struct cxPyramid **table;
} cxPyramidDictionary;
typedef struct cxPyramidReference {
cxCompressType compressType;
union {
struct {
long numIndices;
long *indices;
} cx_compress_multiple;
struct {
long index;
} cx_compress_unique;
} r;
cxPyramidDictionary *dictionary;
} cxPyramidReference;
typedef struct cxPyramid {
cxLattice *baseLattice;
long count;
cxPyramidLayer *layer;
cxPyramidReference ref;
} cxPyramid;
integer cx_compress_none
integer cx_compress_unique
integer cx_compress_multiple
parameter (cx_compress_none = 0)
parameter (cx_compress_unique = 1)
parameter (cx_compress_multiple = 2)
The Pyramid API Routines
Subroutine
Purpose
cxPyrNew
Allocates a pyramid structure
cxConnNew
Allocates a connection list structure
cxLatNew
Allocates a lattice structure
cxPyrSet
Replaces the base lattice in a pyramid
cxPyrLayerGet
Returns the lattice and connection list from a layer of the pyramid
cxPyrLayerSet
Replaces the lattice and connection list from a layer of the pyramid
cxPyrDup
Makes a copy of a pyramid structure
cxConnDup
Copies a connection list structure
cxPyrGet
Returns a pointer to the base lattice and the number of layers from a
pyramid
cxConnEleGet
Returns the connections of an element from a connection list
cxConnEleSet
Sets the connections of an element in a connection list
cxPyrClean
Removes unreferenced items from a pyramid
cxPyrMerge
Selectively merges duplicated elements in a layer
cxPyrLayerSkip
Returns a connection list relating two non-adjacent pyramid layers
cxConnPtrGet
Returns all contents of a connection list
cxConnPtrSet
Sets all contents of a connection list
Subroutine
Purpose
cxPyramidDictionary
Creates a new a pyramid dictionary
cxPyrDictDefault
Calls the default dictionary
cxDictUniqNew
Creates a new a dictionary containing only one kind of element
cxDictMultiNew
Creates a new a dictionary containing more than one kind of element
cxDictElemDefault
Returns the complete default IRIS Explorer dictionary of finite elements
for the given level
cxPyrDictGet
Gets the pyramid dictionary
cxPyrDictSet
Replaces the dictionary in a pyramid
cxDictDescGet
Provides the information required to create a new dictionary
structure
cxPyrCompress
Converts an expanded pyramid to a compressed pyramid
cxPyrDupExpand
Duplicates a pyramid and puts it in expanded form
cxPyrEleDupExpand
Converts an element of a compressed pyramid into an uncompressed element
in its own pyramid
cxPyrConcat
Concatenates one pyramid onto another and expands or merges any
dictionaries they may have
cxPyrEleNormalForm
Removes duplicated nodes and edges, and fixes the faces that contain
removed edges
cxPyrEleBrickForm
Expands each element to 8-node form, adding duplicated nodes
cxDictIndexGet
Finds the "index" of a specified dictionary element
cxDictIndexVGet
Copies a vector of indices for the entire pyramid into "indices"
cxPyrSize
Returns the number of bytes used to store the pyramid
Code Examples
A Simple Example
6
1 3 5 7 9 11
4
0 1 2 5
8
2 4 6 8 10 12 14 16
17
0.0 0.0 0.0 1
1.0 0.0 0.0 2
0.0 1.0 0.0 2
0.0 0.0 1.0 2
2.0 2.0 2.0 2
2.0 2.5 2.0 2
2.5 2.5 2.0 2
2.5 2.0 2.0 2
2.0 2.0 2.8 4
2.0 2.5 2.8 4
2.5 2.5 2.8 4
2.5 2.0 2.8 4
3.0 3.0 4.0 2
3.0 4.0 4.0 2
4.0 4.0 4.0 2
4.0 3.0 4.0 2
3.5 3.5 3.0 1
4
0 1 2 3
8
4 5 6 7 8 9 10 11
5
12 13 14 15 16
C Version:
#include <cx/cxLattice.api.h>
#include <cx/cxParameter.api.h>
#include <cx/cxPyramid.api.h>
#include <cx/Pyramid.h>
#include <cx/DataAccess.h>
#include <cx/DataOps.h>
#include <cx/DataTypes.h>
#include <cx/UI.h>
#include <string.h>
#include <stdio.h>
#include <sys/types.h>
#include <sys/stat.h>
#include <fcntl.h>
#define NUM_TYPES 9
#define NODE(i) ((i==0)?4:i)
long pyr_type[NUM_TYPES] = {
cx_pyramid_dict_quadrilateral,
cx_pyramid_dict_point,
cx_pyramid_dict_line,
cx_pyramid_dict_triangle,
cx_pyramid_dict_tetrahedron,
cx_pyramid_dict_pyramid,
cx_pyramid_dict_prism,
cx_pyramid_dict_wedge,
cx_pyramid_dict_hexahedron,
};
int memclean(cxPyramid *pyr, cxErrorCode ec, cxConnection *conn)
{
if(cxDataAllocErrorGet() || (ec != cx_err_none))
{
if(pyr != NULL)cxDataRefDec(pyr);
if(conn != NULL)cxDataRefDec(conn);
return 1;
}
else
{
return 0;
}
}
void compose(cxLattice *baseLat, char *filename,
cxPyramid **pyr, long quad)
{
cxPyramidDictionary *dict;
cxErrorCode ec = cx_err_none;
cxConnection *conn;
FILE *file;
long *obj = NULL;
long *node = NULL;
long *iptr,i,num_nodes,num_objs,unique,levels;
long show_quad,*elem,*connect;
char buf[100];
if(!filename || filename[0] == NULL)
return;
if((file = fopen(filename,"r")) == NULL)
{
printf(" Error reading file %s\n",filename);
return;
}
/* the object list will not be any larger than the number of nodes */
obj = (long *) cxDataCalloc((size_t) baseLat->dims[0],
(size_t) sizeof(long));
show_quad = FALSE;
num_objs = num_nodes = 0;
while(TRUE)
{
if(fscanf(file,"%ld",&obj[num_objs]) < 0) break;
if(node == NULL)
{
node =
(long *) cxDataMalloc((size_t) obj[num_objs]*sizeof(long));
}
else
{
node = (long *) cxDataRealloc
((void *) node,
(size_t) (num_nodes+obj[num_objs])*sizeof(long));
}
for(i=0;i<obj[num_objs];i++)
{
if(fscanf(file,"%ld",&node[num_nodes+i]) < 1)
{
printf
(" Error reading obj %d. Not enough data\n",num_objs);
return;
}
}
num_nodes += obj[num_objs];
/* determine whether it it a quad or tetra */
if(obj[num_objs] == 4) {
obj[num_objs] = ((quad == 0) ? 0:4);
show_quad = TRUE;
}
num_objs++;
}
/* do I need the radio button? */
if(show_quad)
cxInWdgtShow("Quad");
else
cxInWdgtHide("Quad");
/* am I a unique compressed pyramid ? */
unique = TRUE;
for(i=1;i<num_objs;i++)
{
if(obj[i] != obj[i-1])
{
unique = FALSE;
break;
}
}
/* build the pyramid */
*pyr = cxPyrNew(0);
cxPyrSet(*pyr,baseLat);
levels = 3;
conn = cxConnNew(num_objs,num_nodes);
if(memclean(*pyr,ec,conn)) return;
cxConnPtrGet(conn,NULL,NULL,&elem,&connect);
/* fill elem & connect */
elem[0] = 0;
for(i=0;i<num_objs;i++)
{
elem[i+1] = elem[i] + NODE(obj[i]);
}
bcopy(node,connect,num_nodes*sizeof(long));
/* verify all the nodes are legal */
for(i=0;i<num_nodes;i++)
{
if(node[i] < 0 || node[i] >= baseLat->dims[0])
{
printf("Illegal connection %d at %d\n",node[i],i);
*pyr = NULL;
return;
}
}
/* load all the intermediate levels of the pyramid */
for(i=1;i<levels;i++)
{
cxPyrLayerSet(*pyr,i,NULL,NULL);
}
/* put the connectivity in the pyr */
cxPyrLayerSet(*pyr,levels,conn,NULL);
if(memclean(*pyr,ec,conn))
return;
/* add the compression info */
dict = cxPyrDictDefault(levels);
cxPyramidDictionarySet(*pyr,dict,&ec);
if(memclean(*pyr,ec,NULL))
return;
if(unique)
{
cxPyramidCompressionTypeSet(*pyr,cx_compress_unique,&ec);
if(memclean(*pyr,ec,conn))
return;
iptr = cxPyramidCompressionIndexGet(*pyr,&ec);
if(memclean(*pyr,ec,NULL))return;
*iptr = pyr_type[obj[0]];
}
else
{
/* non-unique */
cxPyramidCompressionTypeSet(*pyr,cx_compress_multiple, &ec);
if(memclean(*pyr,ec,NULL)) return;
cxPyramidNumberIndicesSet(*pyr,num_objs,&ec);
iptr = (long *)cxPyramidCompressionIndexAlloc(*pyr);
if(iptr != NULL)
{
cxPyramidCompressionIndexSet(*pyr,iptr,&ec);
if(memclean(*pyr,ec,NULL))return;
for(i=0;i<num_objs;i++)
{
*iptr++ = pyr_type[obj[i]];
}
}
}
cxDataFree((void *) obj);
cxDataFree((void *) node);
}
Fortran Version:
SUBROUTINE COMPOS(BASLAT,FILNAM,PYR,QUAD)
C
INCLUDE '/usr/explorer/include/cx/DataOps.inc'
INCLUDE '/usr/explorer/include/cx/DataAccess.inc'
INCLUDE '/usr/explorer/include/cx/DataTypes.inc'
INCLUDE '/usr/explorer/include/cx/Pyramid.inc'
INCLUDE '/usr/explorer/include/cx/cxPyramid.api.inc'
C
C .. Parameters ..
INTEGER LSIZE
PARAMETER (LSIZE=4)
C .. Scalar Arguments ..
#if defined(IS_64BIT)
INTEGER*8 BASLAT, PYR, QUAD
INTEGER*8 I1, I2, I3, I4, I5, I6, I7, NUMNOD, NUMOBJ
INTEGER*8 CONN,DICT, EC
INTEGER*8 DIMS(1),CONCT(1), ELEM(1)
#else
INTEGER BASLAT, PYR, QUAD
INTEGER I1, I2, I3, I4, I5, I6, I7, NUMNOD, NUMOBJ
INTEGER CONN,DICT, EC
INTEGER DIMS(1),CONCT(1), ELEM(1)
#endif
CHARACTER*(*) FILNAM
C .. Local Scalars ..
INTEGER I, IER, IOS, IUNIT, J
LOGICAL SHOWQU, UNIQUE
C .. Local Arrays ..
INTEGER NODE(1), OBJ(1),
* PYRTYP(9)
C .. External Functions ..
INTEGER INODE
EXTERNAL CXCONNNEW, CXCONNPTRGET, CXDATAMALLOC,
* CXLATDESCGET, CXPYRAMIDCOMPRESSIONINDEXALLOC,
* CXPYRAMIDCOMPRESSIONINDEXGET, CXPYRDICTDEFAULT,
* CXPYRLAYERSET, CXPYRNEW, CXPYRSET, INODE
C .. External Subroutines ..
EXTERNAL CXINWDGTHIDE, CXINWDGTSHOW,
* CXPYRAMIDCOMPRESSIONINDEXSET,
* CXPYRAMIDCOMPRESSIONTYPESET,
* CXPYRAMIDDICTIONARYSET,
* CXPYRAMIDNUMBERINDICESSET, CXDATAFREE, REALLC
C .. Data statements ..
DATA PYRTYP/CX_PYRAMID_DICT_QUADRILATERAL,
* CX_PYRAMID_DICT_POINT, CX_PYRAMID_DICT_LINE,
* CX_PYRAMID_DICT_TRIANGLE,
* CX_PYRAMID_DICT_TETRAHEDRON,
* CX_PYRAMID_DICT_PYRAMID, CX_PYRAMID_DICT_PRISM,
* CX_PYRAMID_DICT_WEDGE,
* CX_PYRAMID_DICT_HEXAHEDRON/
DATA IUNIT/11/
C .. Pointers to Lattice Structures ..
#ifdef WIN32
POINTER (POBJ,OBJ)
POINTER (PNODE,NODE)
POINTER (PDIMS,DIMS)
POINTER (PELEM,ELEM)
POINTER (PCONCT,CONCT)
POINTER (PNOD,NOD)
#else
POINTER (POBJ,OBJ), (PNODE,NODE), (PDIMS,DIMS)
POINTER (PELEM,ELEM), (PCONCT,CONCT), (PNOD,NOD)
#endif
C .. Executable Statements ..
C
C Open the input file for reading
C
OPEN (IUNIT,FILE=FILNAM,STATUS='OLD',IOSTAT=IOS)
IF (IOS.NE.0) THEN
PRINT *, 'Error opening file ', FILNAM
RETURN
END IF
C
C Get the input lattice description
C Allocate space to hold the associated object list
C
IER = CXLATDESCGET(BASLAT,I1,PDIMS,I2,I3,I4,I5,I6,I7)
POBJ = CXDATAMALLOC(DIMS(1)*LSIZE)
C
C Initialise some variables
C
SHOWQU = .FALSE.
NUMOBJ = 0
NUMNOD = 0
C
C Read the object and nodes until the end of the file is reached
C Allocate space to hold the nodes
C
20 READ (IUNIT,FMT=*,END=40) OBJ(NUMOBJ+1)
IF (NUMNOD.EQ.0) THEN
PNODE = CXDATAMALLOC(OBJ(NUMOBJ+1)*LSIZE)
ELSE
PNOD = PNODE
CALL REALLC(PNODE,PNOD,(NUMNOD+OBJ(NUMOBJ+1))*LSIZE,
* NUMNOD*LSIZE)
END IF
READ (IUNIT,FMT=*,END=40) (NODE(J),J=NUMNOD+1,
* NUMNOD+OBJ(NUMOBJ+1))
NUMNOD = NUMNOD + OBJ(NUMOBJ+1)
C
C Determine if a quad has been entered
C
IF (OBJ(NUMOBJ+1).EQ.4) THEN
IF (QUAD.EQ.0) THEN
OBJ(NUMOBJ+1) = 0
ELSE
OBJ(NUMOBJ+1) = 4
END IF
SHOWQU = .TRUE.
END IF
NUMOBJ = NUMOBJ + 1
GO TO 20
40 CONTINUE
CLOSE (IUNIT)
C
C
C Set the quad widget
C
IF (SHOWQU) THEN
CALL CXINWDGTSHOW('Quad')
ELSE
CALL CXINWDGTHIDE('Quad')
END IF
UNIQUE = .TRUE.
DO 60 I = 2, NUMOBJ
IF (OBJ(I).NE.OBJ(I-1)) UNIQUE = .FALSE.
60 CONTINUE
C
C Build the pyramid structure
C
PYR = CXPYRNEW(0)
IER = CXPYRSET(PYR,BASLAT)
CONN = CXCONNNEW(NUMOBJ,NUMNOD)
IER = CXCONNPTRGET(CONN,I1,I2,PELEM,PCONCT)
ELEM(1) = 0
DO 80 I = 1, NUMOBJ
ELEM(I+1) = ELEM(I) + INODE(OBJ(I))
80 CONTINUE
DO 100 I = 1, NUMNOD
CONCT(I) = NODE(I)
100 CONTINUE
DO 120 I = 1, NUMNOD
IF (NODE(I).LT.0 .OR. NODE(I).GT.DIMS(1)) THEN
PRINT *, 'Illegal connection ', NODE(I), ' at ', I
PYR = 0
RETURN
END IF
120 CONTINUE
IER = CXPYRSET(PYR,BASLAT)
IER = CXPYRLAYERSET(PYR,1,0,0)
IER = CXPYRLAYERSET(PYR,2,0,0)
IER = CXPYRLAYERSET(PYR,3,CONN,0)
DICT = CXPYRDICTDEFAULT(3)
CALL CXPYRAMIDDICTIONARYSET(PYR,DICT,EC)
IF (UNIQUE) THEN
CALL CXPYRAMIDCOMPRESSIONTYPESET(PYR,CX_COMPRESS_UNIQUE,EC)
PCONCT = CXPYRAMIDCOMPRESSIONINDEXGET(PYR,EC)
CONCT(1) = PYRTYP(OBJ(1))
ELSE
CALL CXPYRAMIDCOMPRESSIONTYPESET(PYR,CX_COMPRESS_MULTIPLE,EC)
CALL CXPYRAMIDNUMBERINDICESSET(PYR,NUMOBJ,EC)
PCONCT = CXPYRAMIDCOMPRESSIONINDEXALLOC(PYR)
CALL CXPYRAMIDCOMPRESSIONINDEXSET(PYR,CONCT,EC)
IF (PCONCT.NE.0) THEN
DO 140 I = 1, NUMOBJ
CONCT(I) = PYRTYP(OBJ(I)+1)
140 CONTINUE
END IF
END IF
C
C Free the allocated space for objects and nodes
C
CALL CXDATAFREE(POBJ)
CALL CXDATAFREE(PNODE)
C
RETURN
END
INTEGER FUNCTION INODE(I)
C .. Scalar Arguments ..
INTEGER I
C .. Executable Statements ..
C
INODE = I
IF (I.EQ.0) INODE = 4
C
RETURN
END
SUBROUTINE REALLC(PADDR,PIADDR,NEWSIZ,OLDSIZ)
C
C Reallocate space for the nodes list as it grows
C
INCLUDE '/usr/explorer/include/cx/DataOps.inc'
C
C .. Scalar Arguments ..
INTEGER NEWSIZ, OLDSIZ
C .. Local Scalars ..
INTEGER I
C .. Local Arrays ..
CHARACTER ADDR(1), IADDR(1)
C .. External Subroutines ..
EXTERNAL CXDATAFREE
C .. External Functions ..
EXTERNAL CXDATAMALLOC
C .. Pointers to Lattice Structures ..
#ifdef WIN32
POINTER(PADDR,ADDR)
POINTER(PIADDR,IADDR)
#else
POINTER(PADDR,ADDR), (PIADDR,IADDR)
#endif
C .. Executable Statements ..
C
PADDR = CXDATAMALLOC(NEWSIZ)
DO 20 I = 1, OLDSIZ
ADDR(I) = IADDR(I)
20 CONTINUE
CALL CXDATAFREE(PIADDR)
C
RETURN
END
More Complex Examples
Last modified: Wed Sep 3 14:28:55 1997
[ Documentation Home ]