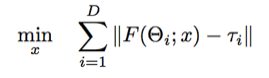In general, the dynamics of a system in terms of the generalized coordinates q can be expressed in the above equation.  Where M, C, g, is the generalized mass, Coriolis and conservative forces matrix, respectively.  The dependence of the dynamics equations on the inertial calibration parameters and the functional relationship between q, its derivatives, and the torque can be made more visually explicit viewing the dynamics equation as:

with:

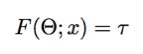
Where m, l, w, and h represents, respectively, each link’s mass, length, width and height.  Now given a data set D, we want to estimate the parameter vector x that minimizes the L2 norm of the difference between the predicted torques and the actual torques:

 

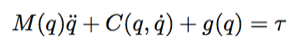
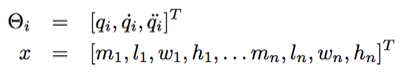
The nonquadratic conjugate gradient solver provided by Cressel Anderson and Levenberg-Marquad algorithm in python’s scipy method does not require knowledge of the gradient nor Hessian of the above function so no further terms needs to be defined.