

 |
AN INTRODUCTION TO NEWTONIAN
MECHANICS by Edward Kluk Dickinson State University, Dickinson ND |
INERTIA, PSEUDOFORCES AND NEWTON FIRST LAW
Introduction
In the applet click on "clear" button, select for
satellite orbit radius 0.20 Gm (1 Gm = 109
m), also select "trace" on, click on
"go" button and "start" button. Watch an
orbit of the selected satellite and rotation of the planet. Now
imagine yourself playing simultaneously roles of two scientists.
One of these scientists is on a planet with several satellites
orbiting this planet on circular orbits. All these orbits are in
the equatorial plane of the planet. Another scientists is on the
board of spaceship observing the planet and its satellites from
very large distance. He sees on the screen of his computer an
image of the planet and its satellites with one satellite at the
same time. For comfort of observation the planet is enlarged 10
times more than the satellitary orbits. Due to this additional
enlargement he can see a white spot near the planetary equator
The equator happens to be along the edge of planetary image. The
laboratory of the first scientist is on the equator. If you draw
on the computer image a perpendicular to the equator line from
this laboratory, it will go straight through the white spot.
Being the scientist on the planet, you just have learned about new discoveries, Kepler third law, Newton second law and law of gravitation. Kepler third law was discovered for planets of your planetary system. Recently using the parallax technique you have measured distances to the satellites of your planet. Now you wonder, is Kepler third law working for the satellites? Especially that you also have other doubts caused by a peculiar behaviour of one of the satellites. This satellite which is about 0.3 Gm from the center of the planet is hanging motionlessly over your laboratory. To see it reset the applet, click on the "clear" button and start it again. Placing the y-axis of the reference frame with its origin at the planet center vertically up and using Newton second law and law of gravitation you can write for this satellite
m Dv / Dt = - G m M / y2 ,
where m and M are masses of the satellite and planet, and y is the distance from the center of the planet to the satellite. Then, because the motionless satellite acceleration Dv / Dt = 0 the left side of this law is zero, whereas the right side is not zero. Evidently something is incorrect there in spite of fact that Newton second law was already positively tested for cases like projectile motion , oscillatory motion and many other cases.
Experimental
Reset and clear the applet again. Select the number of periods equal 5, the tracer off and the orbit radius 1.5 Gm. Prepare your stopwatch, start simultaneously the applet and stopwatch and measure the time used by the satellite to appear again over your laboratory. Recording this time remember that one real second is now equivalent to 104 s in the applet model of the planet with satellites. Record all needed data and results of calculations to fill the first row of the following table
># |
RADIUS OF ORBIT RSAT [m] |
PERIOD T [s] |
(RSAT)3 / T2 |
| 1 | 0.15 x 109 |
||
| 2 | 0.20 x 109 |
||
| 3 | 0.25 x 109 |
||
| 4 | >0.30 x 109 |
Repeat similar measurements for three other satellites. When you are done with it, your conclusion is clear. Kepler third law does not work for these satellites.
But wait a moment. What does it mean a period of the satellite? You have measured these periods in your own frame of reference fixed in your laboratory. This laboratory frame rotates together with your planet. There are, however, other possibilities. For your planetary system planetary periods were referenced to a distant star. You can apply the same reference to the satellites. It is like looking on the planet and its satellites from outside, from a spaceship high above the orbital plane of the satellites. Repeat all your measurements and calculations using the satellite periods referenced to a distant star. This time Kepler third law works even for the hanging (stationary) satellite. So, the results are dependent on a choice of the reference frame. How about a hypothesis that Newton second law does not look the same in all reference frames? There is a possibility of subtle differences which are practically meaningless for some and important for other cases. Well, then it looks like a time for more hard theory.
Investigating Our Hypothesis
Let us take two reference frames (x,y) and (x',y') which are shown in the first figure below.
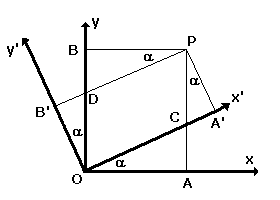
The axis x and y of
(x,y) frame are fixed toward distant stars. The other frame
(x',y') is uniformly rotating together with the planet in
counter-clock direction at a constant angular velocity ![]() . It results with
. It results with ![]() =
= ![]() t.
t.
So far we were using Newton second law in a single dimension, specifically for motions along a straight line. Investigating two dimensional slant projectile motion we have noticed that it was possible to describe a velocity vector for such motion with help of its components (perpendicular projections onto x and y axis of the reference frame). Assuming that such projections will work for any vectors (see the vector A resolution on its components shown in the second figure above) we can postulate a two dimensional Newton second law for the (x,y) frame as follows
mDvx / Dt = Fx (0a), m Dvy / Dt = Fy (0b).
It is instantly visible that it works for a slant projectile motion. If y-axis is directed vertically up and x-axis is horizontal, then Fy = - mg and Fx = 0. Thus, according to the equations which are given above a projectile accelerates down with the acceleration g and its horizontal acceleration stays equal to zero. So, horizontally it moves with a constant speed. And this is what we have learned from our experiments about the projectile motion. But we already know that these equations do not work for a stationary satellite. According to them such satellite should be falling down
Let us assume that this form of Newton second law works in the (x,y) frame introduced in the first figure above. For such case the components vx, vy, Fx and Fy must be taken in the (x,y) frame. Now, if we want to transform this form of Newton second law from the (x,y) to frame to (x',y') frame we have to transform the components of velocity and force between these two frames. Because the velocity components are related to a change of the observed body coordinates and these coordinates are different in these two frames (see the coordinates of the point P in the first figure above) we have to find relations between these coordinates. This is not very difficult but time consuming task.
Looking at the first figure above we can see that
x' = OA' = OC + CA' = OA / cos![]() + PA' tan
+ PA' tan![]() = x / cos
= x / cos![]() + y' sin
+ y' sin![]() / cos
/ cos ![]() ,
,
thus
x = x' cos![]() - y' sin
- y' sin![]() (1a).
(1a).
We also have
y = OB = OD + DB = OB' / cos![]() + BP tan
+ BP tan![]() = y' / cos
= y' / cos![]() + x sin
+ x sin![]() / cos
/ cos![]()
thus
y cos![]() = y' + x sin
= y' + x sin![]() = y' + (x' cos
= y' + (x' cos![]() - y' sin
- y' sin![]() )
= y' (1 - sin2
)
= y' (1 - sin2![]() ) + x' cos
) + x' cos![]() sin
sin![]() =
=
y' cos2![]() + x' cos
+ x' cos![]() sin
sin![]() ,
,
and finally
y = x' sin![]() + y' cos
+ y' cos![]() (1b).
(1b).
The formulae (1 a,b) make possible
to find out coordinates of a point in the (x,y) frame if
coordinates of this point in (x',y') frame and angle ![]() are known. We may call
them a coordinate transformation from (x',y') frame to (x,y)
frame. Multiplying (1 a) by cos
are known. We may call
them a coordinate transformation from (x',y') frame to (x,y)
frame. Multiplying (1 a) by cos![]() and (1 b)
by sin
and (1 b)
by sin![]() ,
and adding them we obtain
,
and adding them we obtain
x' = x cos![]() + y sin
+ y sin![]() (2a),
(2a),
using s similar technique we also can obtain
y' = - x sin![]() + y cos
+ y cos![]() (2b).
(2b).
The formulae (2 a,b) constitute an inverse transformation from (x,y) frame to (x',y') frame.
A next logical step would be to find how
components of velocity and acceleration are transformed between
these two reference frames. The rate of change of x on the left
side of (1a) looks like the x component of velocity
in the (x,y) frame. This rate of change should be equal to the
rate of change of the right side of (1a). But
calculation in this case is not quite simple. The right side
contains two terms, each of them is a product of two time
dependent magnitudes because x', y'
and ![]() are time
dependent. Therefore we are faced with the problem of finding a
rate of change for a product of two time dependent functions.
are time
dependent. Therefore we are faced with the problem of finding a
rate of change for a product of two time dependent functions.
Mark these functions as f(t) and g(t). Then by the definition
D {f(t) g(t)} / Dt = {f(t + Dt) g(t + Dt) - f(t) g(t)} / Dt =
{f(t + Dt) g(t + Dt) - f(t) g(t + Dt) + f(t) g(t + Dt) - f(t) g(t)} / Dt =
[{f(t + Dt) - f(t)} / Dt ] g(t +Dt) + f(t) [{g(t + Dt) - g(t)} / Dt] =
{D f(t) / Dt} g(t) + f(t) {Dg(t) / Dt}
Now we can see that the rate of change for the product of two functions is equal to the rate of change of the first function multiplied by the second function plus the first function multiplied by the rate of change of the second function.
Studying oscillatory motions we already derived another results which can be applied here. Namely
D(sin![]() t) / Dt =
t) / Dt = ![]() cos
cos![]() t and D(cos
t and D(cos![]() t) / Dt= -
t) / Dt= - ![]() sin
sin![]() t .
t .
Finding the rates of change of the both sides of the relation (1 a) we have
Dx / Dt = D(x' cos![]() t) / Dt - D(y' sin
t) / Dt - D(y' sin![]() t) / Dt =
t) / Dt =
Dx' / Dt cos![]() t + x' D(cos
t + x' D(cos![]() t) - Dy' / Dt sin
t) - Dy' / Dt sin![]() t - y' D(sin
t - y' D(sin![]() t) .
t) .
Replacing the rates of change of coordinates by the related components of velocities and using the results for the rates of change of sin and cos functions we obtain
vx
= v'x cos![]() t - v'y
sin
t - v'y
sin![]() t - x'
t - x' ![]() sin
sin![]() t - y'
t - y' ![]() cos
cos![]() t
. (3a)
t
. (3a)
Similarly from the relation (1 b) follows
vy
= v'x sin![]() t + v'y
cos
t + v'y
cos![]() t + x'
t + x' ![]() cos
cos![]() t - y'
t - y' ![]() sin
sin![]() t .
(3b)
t .
(3b)
Thus, velocity components are transforming from the (x',y') frame to the (x,y) frame a more complicated way than the coordinates. But we have to go a one step further and find out how accelerations are transforming. Doing that kind of calculations one has to be very careful not to make a single mistake. Otherwise a final results will not make any sense.
Using the same technique you can calculate step by step the rates of change for both sides of (3 a) and (3 b). This will lead to the following results
Dvx
/ Dt = (Dv'x / Dt) cos![]() t - (Dv'y
/ Dt) sin
t - (Dv'y
/ Dt) sin![]() t -
t -
2![]() (v'x sin
(v'x sin![]() t + v'y
cos
t + v'y
cos![]() t) -
t) - ![]() 2(x'
cos
2(x'
cos![]() t - y' sin
t - y' sin![]() t) (4a)
t) (4a)
Dvy
/ Dt = (Dv'x / Dt) sin![]() t + (Dv'y
/ Dt) cos
t + (Dv'y
/ Dt) cos![]() t -
t -
2![]() (v'x cos
(v'x cos![]() t - v'y
sin
t - v'y
sin![]() t) -
t) - ![]() 2(x'
sin
2(x'
sin![]() t + y' cos
t + y' cos![]() t) (4b)
t) (4b)
At this point you may wonder if we ever obtain from such complicated results anything that is simple and tells us something interesting about the nature. Please be patient and you will see. We still have to go through more mathematics, but there is no any other way. Already Euclid was aware of such problems when he told his king who wanted to learn geometry that there is not a royal way to geometry. In other words certain things are intellectually difficult and if we want to understand them we have to overcome these difficulties. So do not believe in physics without mathematics. No important discovery in physics was ever made without use of mathematics.
A next natural step toward Newton second law in the rotating frame is to plug (4a) and (4b) respectively into (0a) and (0b). The result still looks complicated
m{(Dv'x /
Dt) cos![]() t - (Dv'y
/ Dt) sin
t - (Dv'y
/ Dt) sin![]() t} = Fx
+
t} = Fx
+
2m![]() (v'x sin
(v'x sin![]() t + v'y
cos
t + v'y
cos![]() t) + m
t) + m![]() 2(x'
cos
2(x'
cos![]() t - y' sin
t - y' sin![]() t) (5a)
t) (5a)
m{(Dv'x
/ Dt) sin![]() t + (Dv'y
/ Dt) cos
t + (Dv'y
/ Dt) cos![]() t } = Fy
+
t } = Fy
+
2m![]() (v'x cos
(v'x cos![]() t - v'y
sin
t - v'y
sin![]() t) + m
t) + m![]() 2(x'
sin
2(x'
sin![]() t + y' cos
t + y' cos![]() t) (5b)
t) (5b)
but a substantial simplification is right around
the corner. Let us multiply (5a) by cos![]() t , (5b)
by sin
t , (5b)
by sin![]() t and
add them, then after some algebraic manipulations we obtain
t and
add them, then after some algebraic manipulations we obtain
m Dv'x /
Dt = Fx cos![]() t + Fy sin
t + Fy sin![]() t + 2m
t + 2m![]() v'y +
m
v'y +
m![]() 2x'
(6a).
2x'
(6a).
Taking a good look at the first two terms on the
right side of (6a) and on (2a) we
realise that these two terms probably representF'x
, which is an x component of the force in (x',y') frame. If so,
force components are transformed between (x,y) frame and (x',y')
frame exactly the same way like coordinates of a point.
Multiplying (5a) by - sin![]() t , (5b) by cos
t , (5b) by cos![]() t and adding them
we obtain
t and adding them
we obtain
m Dv'y /
Dt = - Fx sin![]() t + Fy cos
t + Fy cos![]() t - 2m
t - 2m![]() v'x +
m
v'x +
m![]() 2y'
(6b).
2y'
(6b).
Again, the two first terms of the right side of (6b) probably constitute F'y. Therefore Newton second law in the (x',y') frame has the following form
m Dv'x /
Dt = F'x + 2m![]() v'y +
m
v'y +
m![]() 2x'
(7a)
2x'
(7a)
m Dv'y /
Dt = F'y - 2m![]() v'x +
m
v'x +
m![]() 2y'
(7b).
2y'
(7b).
Now it looks like our hypothesis was correct. In
the rotating frame (the (x',y') frame) two additional terms
clearly related through the angular velocity ![]() to the rotation appear. These terms
formally act as additional forces. Will they solve our stationary
satellite problem? What is their general meaning? We need more
investigation.
to the rotation appear. These terms
formally act as additional forces. Will they solve our stationary
satellite problem? What is their general meaning? We need more
investigation.
Back to the stationary satellite
Let us place the origin of the rotating frame in
the center of our planet, its y' axis toward the stationary
satellite and x' axis in the equatorial plane of the planet. This
frame rotates together with our planet and its angular velocity
equals to the angular velocity of the planet. Applying (7a)
and (7b) to the satellite we can see that both
components of its acceleration and velocity are zeros. The
satellite in the rotating frame is at rest. Moreover, F'x
= 0 because gravitational force of
the planet acts on the satellite only along y' axis and x'
= 0 because the satellite is on the y' axis.
Then (7a) becomes a true but nonusefull identity 0
= 0 , and (7b) is reduced to F'y
+ m![]() 2y'
= 0 . Now we can see that the gravitational force
acting on the satellite is equilibrated by one of new
"forces" that have appeared after transformation of
Newton second law from (x,y) frame to (x',y') frame. Thus, at
least formally and qualitatively, the transformed Newtons second
law describes the satellite behaviour correctly. Inserting to the
reduced (7b) the explicit expression for the
gravitational force and denoting the radius of the stationary
satellite orbit by R we obtain
2y'
= 0 . Now we can see that the gravitational force
acting on the satellite is equilibrated by one of new
"forces" that have appeared after transformation of
Newton second law from (x,y) frame to (x',y') frame. Thus, at
least formally and qualitatively, the transformed Newtons second
law describes the satellite behaviour correctly. Inserting to the
reduced (7b) the explicit expression for the
gravitational force and denoting the radius of the stationary
satellite orbit by R we obtain
- G m M / R2
+ m![]() 2R
= 0 or G M / R2
=
2R
= 0 or G M / R2
= ![]() 2R
.
2R
.
At this moment, as the scientist from the planet,
you realise that there are two possibilities to estimate the mass
of your planet. Knowing G, R = 3 x 108
m (see the applet) and ![]() = 10-8
rad/s (see the applet) you can do it using the just
derived relation. But knowing the planetary radius Rp
= 107 m (see the
applet, and remember about additional enlargement of the planet
image) and the gravity acceleration on the planet surface gp
= 9.00 m/s2 the
planetary mass M can be found straight from the
gravitation law. Plugging the data into the respective formulae
you are finding that the mass of your planet calculated using
both methods is 1.35 x 1025
kg (do these calculations, please).
= 10-8
rad/s (see the applet) you can do it using the just
derived relation. But knowing the planetary radius Rp
= 107 m (see the
applet, and remember about additional enlargement of the planet
image) and the gravity acceleration on the planet surface gp
= 9.00 m/s2 the
planetary mass M can be found straight from the
gravitation law. Plugging the data into the respective formulae
you are finding that the mass of your planet calculated using
both methods is 1.35 x 1025
kg (do these calculations, please).
So, it looks like the developed theory and its predictions for the form of Newton second law in the rotating frame (7a,b) are working. Consequently, if gravitational force exerted on the satellite disappears (F'x = F'y = 0), the satellite would move in the (x,y) reference frame along a straight line with a constant speed. This is exactly what the Newton second law (0a,b) for this frame tells you. But from your point of view (the (x',y') frame) this motion is much more complicated. These complications are formally described by the remaining "forces" on the right side of (7a,b). A necessity of the presence of these "forces" in the rotating reference frame (they describe the motion of stationary satellite correctly and give the correct mass of your planet) shows a lack of physical equivalence between the reference frame rotating together with your planet and the reference frame with its axes directed to the distant stars. In the second frame a body which is not acted upon by the other bodies (Fx = Fy = 0), moves along a straight line with a constant speed. But this does not happen in your (rotating) reference frame. Notice that from strictly mathematical point of view if there were no the rest of the Universe represented in our physical case by the distant stars as the references, both our reference frames should be fully equivalent. This means neither of them should be privileged.
Newton first law
Well, we have just deduced Newtons first law.
This law postulates existence of such privileged reference frames
where a body, if not acted upon by the other bodies (Fx
= Fy = 0), moves
along a straight line with a constant speed. These frames are
called inertial frames of reference. A body which does not
interact with other bodies, looked upon from an inertial frame
reveals its inertia, preserving its velocity (speed and its
direction). An amount of inertia is characterized by the inertial
mass of the body. Thus, the additional "forces"
appearing in noninertial reference frames (see (7a,b))
are mathematical descriptions of results of the body inertia.
Sometimes they are called pseudoforces. On the right sides of (7a,b)
there are components of two of them. Namely, Coriolis force with
components (2m![]() v'y
, - 2m
v'y
, - 2m![]() v'x) which
influences winds on our planet and shapes our climate, and
centrifugal force with components (m
v'x) which
influences winds on our planet and shapes our climate, and
centrifugal force with components (m![]() 2x' , m
2x' , m![]() 2y')
which for example keeps stationary satellites on their orbits.
Riding a fast Merry go around we can see and feel this
centrifugal force in action.
2y')
which for example keeps stationary satellites on their orbits.
Riding a fast Merry go around we can see and feel this
centrifugal force in action.
Evaluation
If at this point you :
the objectives of this lesson are fully achieved. If you have doubts try to read it once more concentrating on them, but do not try to memorize this text. Physics is not about memorizing, it is about understanding.
| Last update: March 24, 1997 | E - mail to Edward Kluk |
| Copyright (c) 1996 Edward Kluk | |