 |
AN
INTRODUCTION TO NEWTONIAN MECHANICS by Edward Kluk Dickinson State University, Dickinson ND |
KEPLER THIRD LAW, NEWTON SECOND LAW AND NEWTON LAW OF GRAVITATION
Introduction
For thirty years Tycho
de Brahe (1546 - 1601) was recording positions of planets on
the celestial sphere. His purpose was to prove his own geocentric
model of the universe with the sun orbiting the earth and rest of
the planets orbiting the sun. But after Tycho's death
his assistant Johannes Kepler (1571 - 1630)
used these data to generalize the heliocentric model of Nicolaus
Copernicus (1473 - 1543) . Applying mathematical method of
analysis he established that the planetary orbits are elliptical
(not quite circular as it was assumed by Copernicus). He also
proved that for any two planets their periods (times needed to
accomplish one full revolution around the sun) T1
and T2 and
their average distances from the sun R1
and R2 are
fulfilling the following relation
(T1 / T2) 2 = (R1 / R2) 3.
This relation is known as Kepler third law. A half of a century later Newton derived it from his second law an law of gravitation.
You may wonder how Kepler could know the distances of the planets from the sun. As a matter of fact he did not. But using Tycho's data and trigonometry he was able to find the ratios R1 / R2 for some pairs of planets. In the first figure below it is explained how he could do it. Dealing with inner planet (a planet that has its orbit inside of the earth orbit) it is enough to find a maximal
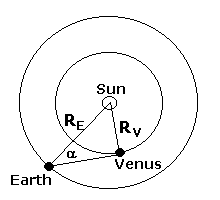
angular distance 
between this planet
and the sun. Than from the figure above follows R
V / R E =
sin,
and the ratio can be easily calculated. Practically, however,
finding the angle
is not quite simple because one has to know direction
toward the sun when the sun is still below the horizon. Otherwise
the planet will not be visible. Nevertheless 16 century
astronomers new how to make this kind of measurements.
Experiment
A main purpose of this
"experiment" is to show how uncomplicated would be a
discovery of Kepler third law for an observer who has a lot
of time and is placed outside of our solar system. The solar
system presented in the applet has seven planets orbiting their
sun along circular orbits. But you can see only one planet at a
given time. Distances in this planetary system are shown in Tm
(1 terameter = 10 12m).
To make properties of this system comparable to the
properties of our solar system we will assume that one second of
the real time is equivalent to a 10 4
days for the planetary system of the applet.
Start the applet clicking on the clear button. Notice that besides one planet and the sun (star) you have there an arrow showing direction to another, very distant star. We need this direction as a reference to measure how long it takes for any of these planets to make a one full revolution. Notice that if you try to measure how fast you can make one round on a track, you automatically (without thinking about it) select a reference direction. Without such reference it is impossible to figure out when a one full revolution is made. If you have any doubts make a simple experiment. Stand in the middle of your living room, close your eyes and screen them well with your hands. Make a few turns about your own vertical axis and try to stop when you face your starting direction. If by chance you have made it, try it again.
Going back to the applet experiment, select any possible radius of a planetary orbit and a single revolution. Click "go" for acceptance of your choice. Now simultaneously click "start" and start your stopwatch. Record the orbit radius in meters and period of the selected planet in make believe seconds in a table similar to the one which is placed below. Remember, a real second is treated in this "experiment" as 10,000 full days or 8.64 x 10 8 make believe seconds. Calculate R3 / T2 . Repeat all of it for three more planets selecting different radii of orbits.
| # | ORBIT RADIUS R (m) | PERIOD T (s) | R3 / T2 |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 |
Compare values of R3/ T2for different planets. If everything was done correctly you should rediscover Kepler third law. Well, it was ease, was not it?
Now think about Brahe and Kepler. They had much more difficult task than you because measurements and calculations were made from inside of the system and in a real time. The fact that the earth is not only revolving around the sun, but also rotating about its axis which is not even perpendicular to the plane of the earth orbit, makes a picture of planetary motion very complicated. This is why we should admire Brahe and Kepler's experimental and mathematical skills.
Kinematics
of circular motion
If a body moves with a constant speed along
a circular orbit, it is still accelerating because its
velocity continuously changes. Remember, velocity is a vector and
a rate of velocity change is an acceleration.
Body's velocity tells you not only about actual speed of
this body (the velocity vector magnitude or length) but also
about actual direction of motion. The diagram below shows how a
body's velocity changes. For this particular motion the
velocity magnitude does not change but the velocity direction
does change. This change 
v is explicitly shown in the right part
of the diagram. Because the vectors OA and v1
as well as vectors OB and v2 are
perpendicular the triangle OAB and the
triangle made of vectors v1
, v2 and v are
similar (here for convenience vectors are marked by bold letters
and their magnitudes by bold and italic letters).
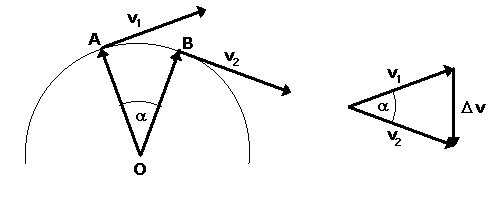
This similarity leads to the following proportion for vector magnitudes
v / v1
= AB / r ,
where the circle radius r
= OA. Dividing both sides of this proportion by
a time t
used by the body to cover the distance from A
to B we obtain
(v / t) / v = (AB / t) / r .
For sake of simplicity v1
is replaced here by v because all velocities for
this case have the same magnitudes. Making t very
small we also make v and AB very
small. Then, according to our convention, they can be replaced by
Dt, Dv and Dx, where Dx
is a length of the AB arc. When the points A
and B are very close the distance between them
hardly differs from the length of arc AB. It
results with
(Dv / Dt) / v = (Dx / Dt) / r or Dv / Dt = v2 / r
because Dx / Dt = v . At this point we may suspect that Dv / Dt is a magnitude of centripetal acceleration of the body resulting from a force that keeps this body on its circular trajectory. Moreover, looking at the figure above we may make an educated guess that this acceleration is directed toward the center of the circle. We cannot, however, be sure of it because our math is not formal enough.
Newton law of gravitation
Close enough to the surface of Earth its
gravitational force which pulls everybody toward the Earth center
seems to be independent of a body's altitude. After all
acceleration of freely falling bodies is constant. But here we
are talking about change of a distance that is very small even if
compared to the radius of Earth (~6400 km). It
would be too naive to assume that gravitational force between Sun
and a planet or Earth and Moon does not depend on the distance.
Let us assume a proportionality of such force to R
-n where R is a distance
between two interacting bodies and n is
a number. Such assumption takes formally into consideration wide
range of possibilities. For example, if n < 0
the gravitational force would be increasing with the
distance. The relation F = mg
suggests that the gravitational force should be
proportional to the masses of both interacting objects. This
becomes very apparent considering two hypothetical
identical planets. If this force is proportional to the mass of
one planet it also should be proportional to the mass of the
other planet. Therefore the gravitational force can be postulated
as
FG = G m1 m2 / R n
where G is a constant (now known as the universal gravity constant) and m1, m2 are masses of interacting objects. The universal gravity constant was measured first time in a laboratory by Henry Cavendish (1731-1810). Its actually accepted value is G = 6.67259 x 10 -11 m3 kg-1 s-2.
If such a force acting between the sun (mass M) and planet causes a centripetal acceleration of the planet (mass m), then according to Newton second law (ma = F)
m v2 / R = G m M / R n
Here for sake of simplicity we
have assumed a circular orbit for the planet. As a matter of fact
most planetary orbits in our solar system are almost circular.
Thus, the speed of the planet v = 2
R / T, where T
is a period of one full revolution of the planet around the
sun. Inserting v to the Newton second
law for the planet and rearranging this equation we obtain
R n+1
/ T2 = G M / (2)2
.
The right side of this relation does not contain any reference to the planet. Therefore the ratio on the left side is the same for any planet orbiting the sun on a circular orbit. Denoting radii and periods for chosen two planets as R1 , R2 and T1 , T2 respectively, and performing simple algebraic manipulations we get
(R1 / R2)n+1 = (T1 / T2)2.
Comparing this theoretical result with Kepler third law forces us to accept n = 2 which leads to
FG = G m1 m2 / R 2.
This way we have rediscovered Newton law of gravitation.
Problem of weight revisited Gravitation law in its form presented above was deduced for objects with sizes much smaller than a distance between them. What if we want to apply it to a man on the earth surface, a flying plane or an artificial earth satellite? For such cases the condition formulated above is not fulfilled. There is, however, a possibility of using of gravitation law for these cases. We always can abstractly divide the earth and the other object into small enough pieces and apply this law separately to every pair of such pieces, one piece of earth and one piece of object. But now we have another serious problem. How to add all these gravitational forces acting between all pairs together. Here again, advanced mathematics comes to the rescue. If we knew Carl Friderich Gauss (1777-1855) theorem and had assumed a spherical symmetry of the mass distribution inside of the earth as well as small size of the object in comparison with the earth size, we could show that the discussed gravity force would have the following form
FG = G m M / R2 = m [G M / R2] = m g(R)
where m and M are masses of the object and the earth, and R is the distance between the earth center and the object. Last two rearrangement of this formula make it almost identical with the formula F = mg . Except that in the new formula the gravity acceleration g(R) depends on the distance of the object from the earth center whereas g seems to be constant.
To examine how pronounced is the dependence of g(R) on R let us apply a simple mathematical analysis. If the object is at height h over the earth surface and the earth radius is denoted as Re , then R = Re + h. It results with
g(R) = G M / (Re + h)2 = {G M / (Re)2} / (1 + h / Re)2.
Here the numerator (in the figure brackets) represents gravity acceleration right on the surface of the earth, and denominator describes a change of this acceleration if the body is lifted to the height h over the earth surface. To estimate how big this change might be let us assume h = 10 km = 104 m and calculate the ratio
g(Re + h) / g(Re) = (1 + h / Re) -2 = (1 + 10/6400) -2 = 0.9969 .
Such small difference is very hard to measure. This is why for most practical applications we are assuming that g is a constant.
The same kind of correction for Shuttle which flies 320 km above the surface of the earth is quite substantial because the same ratio for h = 320 km equals 0.952 . Thus, the gravity acceleration there is about 5% less than on the earth surface. To find why astronauts fill weightless go to our next lecture.
Evaluation
If at this point you :
the objectives of this lesson are fully achieved. If you have doubts try to read it once more concentrating on them, but do not try to memorize this text. Physics is not about memorizing, it is about understanding.
| Last update: March 10, 1997 | E - mail to Edward Kluk |
| Copyright (c) 1996 Edward Kluk | |
