AN INTRODUCTION TO NEWTONIAN MECHANICS by Edward Kluk Dickinson State University, Dickinson ND

PENDULUM, INERTIAL AND NONINERTIAL REFERENCE FRAMES

     Introduction
      Discovering existence of inertial and noninertial reference frames we have learned that Newton second law describing planar motion in an inertial (x,y) reference frame

m Dv_x / Dt  =  F_x           (0a),       m Dv_y  / Dt  =  F_y             (0b)

when transformed to a uniformly rotating (x',y') reference frame, takes a new form that includes Coriolis and centrifugal pseudoforces

m Dv'_x / Dt  =  F'_x  + 2mv'_y + m²x'       (1a)

m Dv'_y / Dt  =  F'_y  -  2mv'_x + m²y'       (1b).

These pseudoforces are formally describing effects of body's inertia as seen from a rotating reference frame. With their help we have explained a phenomenon of stationary satellites.

      Now we will try to learn how an ordinary pendulum behaves in inertial and noninertial reference frames. We are considering a reference frame as inertial if its axes have directions toward fixed distant stars.

     Pendulum in an inertial reference frame

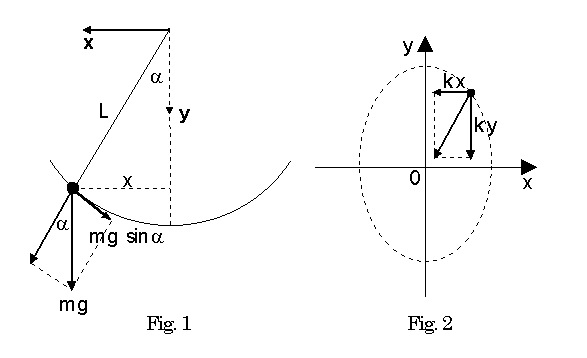
      In Fig. 1 there is presented a pendulum swinging along the circular arc of radius L. The gravity force mg acting upon the pendulum is resolved into two components. The component along the pendulum string is neutralized by a strength of the string, so it does not influence the pendulum motion. The other component  mg sin  pulls the pendulum along the circular arc toward its bottom (equilibrium) point. This component is a net force F acting on the pendulum. It can be resolved into its components F_x and F_y along x and y axis respectively. These components are

F_x = - mg sincos        and         F_y  =   mg sinsin .

      Inserting these components into Newton second law for inertial frames of reference (0a), (0b) we have

m Dv_x / Dt  =  - mg sincos          (2a),       m Dv_y  / Dt  =  mg sinsin .            (2b)

Canceling masses on both sides of each equation we can instantly conclude that the pendulum motion is independent of the pendulum mass. Generally, however, this set of equations is too difficult to be discussed here without a substantial simplification. Limiting pendulum swings to small angles (less than  11.5^o   or   0.2  radians)  we  notice  that a maximum of the force in the equation (2b) is much smaller than in the equation (2b). Check it on your calculator finding values of cos and sin.  This means that  accelerations, velocities and displacements in y direction  are very small and can be disregarded. Also cosin the equation (2a) can be replaced by 1. Then, the simplified equation (2a) can be rewritten as follows

Dv_x / Dt  =  - g sin= -(g/L) L sin =  - (g/L) x .         (3)

But this looks like the equation for a harmonic oscillator with the spring constant k = g/L and  mass m = 1 kg. Thus, the period  T  for such pendulum is given by

T  =  2(L/g)^½ ,         (3a)

and  x displacement from equilibrium point is

x(t)  =  x_o cos(t) ,  where   =  (g/L)^½ .      (3b)

      Now it is a time for a first real experiment. Make at least 1 m long pendulum using thin strong string and rather heavy machine screw nut. Arrange a point like fixed suspension with the freedom of swinging in any vertical plane. Measure the pendulum length  L  from the suspension point to the center of the nut. Measure with a stopwatch elapsed time for ten full swings counting swings very carefully. Make two more such measurements. The results should be almost identical. If they differ substantially, you probably have miscounted swings. Find from your data an average period  T  for a single swing. Knowing  L  and  T  calculate the gravity acceleration  g. You should be off its value of  9.8 m/s² no more than 2%. This means that our theory works.

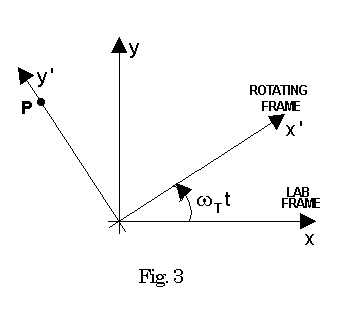
      So far we were assuming that the pendulum swings only in a single vertical plane. But if realising the pendulum you give it a small side push it will be moving along an oval path on the spherical surface with the radius  L . Let us assume that the plane x,y in Fig. 2 is tangential to the mentioned above sphere at the pendulum equilibrium point O. Notice, we have changed the meaning of y-axis !!! Now the unmarked force in Fig. 2 pulling the pendulum toward its equilibrium position, if we are regarding only a small swings, has the magnitude  F  =  k (x² + y²)^½  ( the force is proportional to the pendulum distance from the equilibrium point) and its components are  F_x  =  - k x  and  F_y  =  - k y . Here  x  and  y  are coordinates of the pendulum and  k  =  g/L. Applying to this situation Newton second law (0a,b) we have

Dv_x / Dt  =  - kx          (4a),       Dv_y  / Dt  =  - ky            (4b).

It means that each coordinate of the pendulum behaves like a harmonic oscillator. We have already found a solution of (4a) . This solution is  x(t)  =  x_o cost . Thus (4b) has a solution   y(t)  =  y_o cost . Using exactly the same method  the additional solutions

x(t)  =  x_o sint   and    y(t)  =  y_o sint

can be found.

      Now imagine yourself starting the pendulum from the intersection of  x-axis and the oval trajectory in Fig. 2. If you just let it go without any additional push, then its y coordinate will be always zero and x coordinate will be described by the function  x(t)  =  x_o cost . But if you induce an initial velocity  v_o  in  y direction, then the y coordinate will not stay equal to zero. Then the only possible choice is to take  y(t)  =  y_o sint  because we must also have  y(0) = 0. To find a shape of trajectory let us make the following simple calculation

[x(t)/x_o]² + [y(t)/y_o]²  =  [cost]² + [sint]²  =  1.

Thus this trajectory is an ellipse with the semiaxes  x_o  and  y_o. If  y_o =  x_o the ellipse becomes a circle.

      In our particular case  y_o depends on  v_o . A relation between them follows from the y component of pendulum velocity. This component

v_y(t)  =  Dy(t)/Dt  =  D[y_o sint]/Dt  =  y_o cost ,

thus  y_o  =  v_o /. Then this particular motion of the pendulum is described as follows

x(t)  =  x_o cost   and    y(t)  = ( v_o /) sint           (5a).

If the pendulum starts from y axis with an initial velocity in opposite direction to the direction of x axis, then its motion is described by

x(t)  =  - (v_o /) sint   and    y(t)  =  y_o cost           (5b).

      Pendulum in a rotating reference frame   

      Suppose that the pendulum is fixed on a slowly rotating turntable and the pendulum suspension is placed exactly on the rotation axis of the turntable. In Fig.3 there are shown two reference frames. The lab frame fixed in the lab and rotating frame fixed on the turntable. The origins of both frames are exactly on the rotation axis of the turntable. Initially the pendulum bob is at the point P in the rotating frame. The pendulum is released from the turntable without any push

at the instance  t = 0 when both reference frames overlap. If we disregard the earth rotation, the subsequent motion of the pendulum as seen from the lab frame is described by the equations (4a,b) and (5b). The initial speed  v_o  in the negative x direction as seen from the lab frame is related to y_o  (the distance of point P  from the origin of rotating reference frame) and _T (the angular speed of the turntable), and  v_o = y_{o T} . Therefore an observer placed in the lab frame will see a trajectory of the pendulum as an ellipse with the semiaxis y_o along  y axis and the semiaxis  y_{o T} / along  x axis.

      But can we disregard the earth rotation? Studying a relatively slow motion in a time interval of a few minutes we can because centrifugal and Coriolis forces related to the earth rotation are very small. They are proportional to the angular velocity of the earth, and the square of this velocity, respectively. This velocity is only 7.27 x 10^-5 rad/s. Therefore its effects in a short time interval are hardly measurable. In a long time interval, however, they cumulate and become well visible.

      The same motion seen by an observer in the rotating frame is described by prohibitively looking equations (1a,b). Luckily enough we do not need to solve them. We already know how coordinates x,y of the pendulum evolve in time in the lab frame, and we also discovered lately how they can be transformed from the lab frame to the rotating frame. The transformation formulae as applied to the present situation have the following form

x'  =  x cos _T t + y sin_T t              (6a),

y'  =  - x sin_T t + y cos_T t               (6b).

Inserting into them x and y as described by the equations (5b) with v_o = y_{o T}  we obtain

x'(t)  =  y_o[- (_T /) sint cos_T t + cost sin_T t ]           (7a),

y'(t)  =  y_o[(_T /) sint sin_T t + cost cos_T t ]             (7b).

This result looks still very complicated and practically impossible to visualize without graphing. Some conclusions are easier to reach if it is reshaped with help of trigonometric relations like cos a  cos b = (1/2)[cos(a+b) + cos(a-b)]  etc. Then

x'(t)  =  (yo/2)[1 - (_T /)] sin(+_T)t  -  (yo/2)[1 +(_T /)] sin(-_T)t      (8a),

y'(t)  =  (yo/2)[1 - (_T /)] cos(+_T)t  +  (yo/2)[1 +(_T /)] cos(-_T)t      (8b).

According to this result the pendulum motion seen from the rotating frame is a superposition of two simple motions, clockwise circular motion with the radius (yo/2)[1 - (_T /)] and angular frequency +_T,  and counterclockwise circular motion with the radius (yo/2)[1 + (_T /)] and angular frequency -_T . Here we are observing a rotational Doppler shift. The pendulum seen from the lab frame exhibits a single angular frequency , whereas in the rotational frame it exhibits two shifted frequencies +_T  and  -_T . Its original angular frequency is modulated by the angular frequency _T  of the turntable.

      In a particular case when = _T  the result is very simple  because  (8a,b) are reduced to x'(t)  = 0   and   y'(t)  =  (yo/2)[1 + (_T /)] =  y_o .  So, in the rotating frame the pendulum stays at rest because a centrifugal force acting upon it equilibrates the component of gravity force that pulls the pendulum toward the turntable rotation axis. This is a very similar case to the stationary satellite case.

      Now you are ready to simulate with help of included applet some pendulum trajectories as they are seen from lab and rotating frames. For the simulation the formulae (8a,b) are used. Do not forget that this pendulum always starts from a rest in the rotating frame.

      Set the pendulum period  T_p to 10 s and the turntable rotation period T_t also to 10s. This means that = _T , and in the rotating frame the pendulum should stay at rest whereas in the lab frame it should have a circular trajectory. After running this case in the rotating frame click "reset" and select the inertial (in this case lab) frame. A change of the frame resets other parameters, so you have to restore them to desired values. Run it to see what you are expecting to see. Now clear the view window and make two new experiments taking  T_p=5s , T_t = 10s  and  T_p=5s , T_t = 50s . Conclusions from the obtained patterns are obvious. A smaller ratio of  T_p / T _t  leads to a narrower elliptical trajectory in the inertial reference frame and a trajectory with more spikes in the rotating frame. Imagine replacing the turntable by our planet Earth, placing a very long pendulum on the North Pole and directing x and y-axes of an inertial frame toward two fixed stars. Well, we have a Foucault pendulum on North Pole. If our pendulum is 100 m long its period would be only 20 s whereas earth rotational period is 86400 s. Thus, its trajectory viewed from the inertial frame would be an exteremely elongated ellipse with its longer axis/shorter axis ratio equal to 4320. The same trajectory viewed from the earth would have 8640 spikes per 24 hours. Hopefully you understand now how Foucault pendulum works but you must admit that the understanding process is neither simple nor short. And this one is probably the simplest and shortest if you start from scratch.

      So far we were investigating pendulum motions with  T_p / T _t  ratio smaller or equal one. Evidently for these cases initial centrifugal force is smaller than initial force pulling the pendulum toward the rotation axis. This is why, the pendulum initially "falls" toward the rotation axis but misses it being redirected by Coriolis and centrifugal forces. For  T_p / T _t  ratio greater than one pendulum trajectories in the inertial frame are still elliptical but their views in the rotating frame is quite different. Examine two such cases taking  T_p = 20s , T_t = 10s with two turns and  T_p=50s , T_t = 10s with three turns. This time initial centrifugal forces are greater than initial forces pulling the pendulum toward the rotation axis. It results in initial motion away from the rotation axis.

      The most important conclusion following from our investigation of pendulum motion is that it provides information about reference frames. It tells us how much inertial or noninertial a given frame of reference is or, to what extend we may apply in it Newton second law without taking corrections for pseudoforces. You have to be aware that we really do not know if ideally inertial frames exist. We only know that some reference frames are more inertial than the others. In these more inertial frames Newton second law correctly predicts motions for longer time intervals. For most engineering problems reference frames fixed on the earth surface are enough inertial. But long range artillery shells are influenced by Coriolis force due to their high speed and relatively long time of flight.

      Pendulum in vertically accelerating reference frame 

       Motion of pendulum is influenced not only by a rotation of the reference frame but also by a linear acceleration of such frame. Let us assume that (x,y)-frame in Fig.4 is an inertial frame. The pendulum is fixed in (x',y')-frame accelerating vertically with a constant acceleration a . A real case of such situation could be arranged in an accelerating elevator. But practically elevators cannot accelerate for too long.  In (x,y)-frame the pendulum motion will be described with help of  the equations (0a,b) with properly chosen net force components  F_x  and  F_y.

      The relations between the pendulum coordinates in both reference frames are following (see Fig.4)

x(t) = x'(t),     y(t) = y'(t) + y_o(t)  where  y_o(t) = y_o(0) + (a/2) t² .

Here  y_o(0)  describes position of (x',y') frame with respect to (x,y) frame at  t = 0. Then

v_x(t) = Dx(t)/Dt = Dx'(t)/Dt = v'_x(t)  and  v_y(t) = Dy(t)/Dt = Dy'(t)/Dt + a t = v'_y(t) + a t .

Consequently

Dv_x(t)/Dt = Dv'_x(t)/Dt    and    Dv_y(t)/Dt = Dv'_y(t)/Dt + a .       (9)

The net force components acting on the pendulum contain components  T_x  and  T_y  of the force exerted by the string and gravity force. Therefore they can be presented as follows

F_x = T_x   and  F_y = T_y - mg .         (10)

Inserting the relations (9) and (10) into (0a,b) we obtain the equations describing pendulum motion in (x',y')-frame

m Dv'_x / Dt  =  T_x           (11a),       m Dv'_y  / Dt  =  T_y - m(g + a) .          (11b)

Inserting the relations (10) into (0a,b) the equations describing pendulum motion in (x,y)-frame are obtained

m Dv_x / Dt  =  T_x           (12a),       m Dv_y  / Dt  =  T_y - mg.          (12b) .

But the equations (11a,b) and (12a,b) differ only by the term - ma in (11b). Therefore motion of pendulum fixed in (x',y')-frame looks almost like motion of the same pendulum fixed in (x,y)-frame except that in (x',y')-frame on a top of the gravity force - mg  there is an additional pseudoforce - m a. This new pseudoforce describes a well known inertial effect. Put on a smooth horizontal surface a sheet of smooth paper and on this paper a heavy smooth object. Pull quickly this sheet in a horizontal direction. If you pull it fast enough, the object will not move whereas the sheet of paper will. If an actual acceleration of the sheet of paper is  a , with respect to a reference frame placed on this paper the object moves with an acceleration  - a .  Then, it looks like a force of  - ma  is acting on the object in this reference frame.

      We have already solved the equations (0a,b) for a pendulum with small swings. But the equations (12a,b) are the same as (0a,b) for a pendulum. Then for small swings the pendulum period is given by the formula  (3a) and  x coordinate of the pendulum varies in time according to the formula (3b).  Almost the same solution apply also to the equations (11a,b) . The only difference is that we have to replace  g  by  g + a . This replacement is a clear consequence of comparison of (11b) and (12b). Therefore for a pendulum in the accelerating reference frame

T  =  2{L/(g + a)}^½ ,         (13a)

and

x'(t)  =  x'_o cos(t) ,  where   =  {(g + a)/L}^½ .      (13b)

Therefore the pendulum in the accelerating reference frame (x',y') feels this acceleration as an additional "gravitational" field. This field can be positive or negative. If the (x',y')-frame is freely falling down, then  a = - g  or  g + a = 0 , consequently   =  0    and   x'(t)   stays constant. So  the pendulum appears to be weightless in this frame.  The same kind of weightlessness are experiencing astronauts on the board of orbiting Shuttle or Mir station. But there the earth gravity acceleration is neutralized by another pseudoforce which is a centrifugal force. Notice, the reference frames like freely falling elevator, Shuttle or Mir station (if they are not rotating) look remarkably like inertial frames where Newton second law without inclusion of pseudoforces is valid. The last statement is a simplified form of principle of equivalence  which assumes identity of physics laws in inertial frames and mentioned above frames.

      Start the incorporated applet, select vertically accelerating frame with the tracer off and measure ten pendulum periods for the following accelerations: - 4.9, 4.9, 9.8 and 19.6 m/s². Compare your results with predictions given by the formula (13a).

     Evaluation

       If at this point you :

• can derive or make an educated guess how a formula for the pendulum period in horizontally accelerating frame should look like (help yourself with Fig. 5) and verify it using the incorporated applet

the objectives of this lesson are fully achieved. If you have doubts try to read it once more concentrating on them, but do not try to memorize this text. Physics is not about memorizing, it is about understanding.

Since February 1997 you are visitor