Here is the geometry of the simulation:
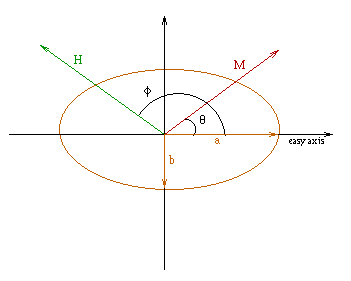
H: external field
M: magnetization of the particle
Theta: angle between easy-axis and magnetization
Phi: angle between easy-axis and external field
a,b: half-axes of the particle
The Energy-density of a ferromagnetic particle is calculated
while a magnetic field H is applied to the particle. Searching
the local minimum of the energy provides the angle that the
magnetization forms with the easy-axis. The Hysteresis-loop is a
result of the variation of the applied field.
Here is the geometry of the simulation:

H: external field
M: magnetization of
the particle
Theta: angle between easy-axis and magnetization
Phi: angle between easy-axis and external field
a,b: half-axes of
the particle
The energy of the particle consists of the Zeeman-energy,
the energy due to crystal-anisotropy and shape-anisotropy:
E = EZ + EC
+ ES
The energy due to interaction with the external field
calculates:
EZ = -µ0
MS H cos(theta-phi)
MS: saturation magnetization
Uniaxial Anisotropy:
EC = K1
sin2(theta) + K2
sin4(theta) + ...
Biaxial Anisotropy:
EC = K1
cos2(theta) sin2(theta)
+ ...
The order of magnitude of K1 is for cubic crystals
about 103 - 104 [J/m3] and for
hexagonal crystals about 105 - 106 [J/m3].
(see [Jäger])
[The simulation only pays attention to K1]
The energy of Demagnetization-field calculates:
ES = 1/2 µ0
MS2
(Na cos2(theta)
+ Nb sin2(theta))
Na: Demagnetization-coefficient parallel
to the easy-axis
Nb: Demagnetization-coefficient perpendicular
to the easy-axis
The coefficients for simple shapes:
Sphere:
Na = Nb (= Nc) = 1/3
Infinite layer:
Ni = 0 (in the layer)
Ns = 1 (perpendicular to the layer)
Ellipsoid:
For a ellipsoid with the half-axes a > b >> c (see [Morrish]) the coefficients
are:
Na = pi c [1 - (a-b)/4a - 3 ((a-b)/4a)2]/4a
Nb = pi c [1 + 5(a-b)/4a + 21 ((a-b)/4a)2]/4a
Na + Nb + Nc = 1
If your browser can't run 1.0 Java applets, here is a picture of the applet
[Morish] : A.H. Morrish The
physical principles of magnetism
[Wernsdorfer]: W. Wernsdorfer, Magnéé ą micro-SQUID pour
l'é de particules ferromagné isolé aux é sub-microniques,
C.N.R.S.-Grenoble (1996)
[Jäger] : E. Jäger, R. Perthel, Magnetische
Eigenschaften von Festkörpern, Akademie Verlag (1996)