Visualizing Complex Hypermedia Networks through Multiple Hierarchical Views
Visualizing Complex Hypermedia Networks through Multiple Hierarchical Views
Sougata Mukherjea, James D. Foley, Scott Hudson
- Graphics, Visualization & Usability Center
- College of Computing
- Georgia Institute of Technology
- E-mail: sougata@cc.gatech.edu, foley@cc.gatech.edu, hudson@cc.gatech.edu
- ABSTRACT:
- Our work concerns visualizing the information space of hypermedia systems using
multiple hierarchical views. Although overview diagrams are useful for helping the user to
navigate in a hypermedia system, for any real-world system they become too complicated
and large to be really useful. This is because these diagrams represent complex network
structures which are very difficult to visualize and comprehend. On the other hand,
effective visualizations of hierarchies have been developed. Our strategy is to provide
the user with different hierarchies, each giving a different perspective to the underlying
information space to help the user better comprehend the information. We propose an
algorithm based on content and structural analysis to form hierarchies from hypermedia
networks. The algorithm is automatic but can be guided by the user. The multiple
hierarchies can be visualized in various ways. We give examples of the implementation of
the algorithm on two hypermedia systems.
- KEYWORDS:
- Hypermedia, Overview Diagrams, Information Visualization, Hierarchization.
INTRODUCTION
Overview diagrams are one of the best tools for orientation and navigation in hypermedia
documents [17]. By presenting a map of the underlying
information space, they allow the users to see where they are, what other information is
available and how to access the other information. However, for any real-world hypermedia
system with many nodes and links, the overview diagrams represent large complex network
structures. They are generally shown as 2D or 3D graphs and comprehending such large
complex graphs is extremely difficult. The layout of graphs is also a very difficult
problem [1]. Other attempts to visualize networks such as
Semnet [3], have not been very successful.
In [13], Parunak notes that: "The insight for hypermedia is
that a hyperbase structured as a set of distinguishable hierarchies will offer
navigational and other cognitive benefits that an equally complex system of
undifferentiated links does not, even if the union of all the hierarchies is not itself
hierarchical." Neuwirth et al. [12] also observed that the
ability to view knowledge from different perspectives is important. Thus, if different
hierarchies, each of which gives a different perspective to the underlying information can
be formed, the user would be able to comprehend the information better. It should be also
noted that unlike networks some very effective ways of visualizing hierarchies have been
developed. Examples are Treemaps [7] and
Cone Trees [15].
This paper proposes an algorithm for forming hierarchies from hypermedia graphs. It uses
both structural and content analysis to identify the hierarchies. The structural analysis
looks at the structure of the graph while the content analysis looks at the contents of
the nodes. (Note that the content analysis assumes a database-oriented hypermedia system
where the nodes are described with attributes). Although our algorithm is automatic,
forming the "best" possible hierarchy representing the graph, the user can guide the
process so that hierarchies giving different perspectives to the underlying information
can be formed. These hierarchies can be visualized in different ways.
Section 2 presents our hierarchization process. Section 3 shows the implementation of
the algorithm in the Navigational View Builder, a system we are building for
visualizing the information space of Hypermedia systems
[10], [11]. This section
discusses the application of the algorithm on a demo automobile database and a section of
the World-Wide Web. Section 4 discusses how the hierarchies can be transformed to
other forms of data organizations. Section 5 talks about the related work while section 6
is the conclusion.
THE HIERARCHIZATION PROCESS
New Data Structure
For our hierarchization process we use a data structure which we call the pre-tree.
A pre-tree is an intermediate between a graph and a tree. It has a node called the
root which does not have any parent node. However, unlike a real tree, all its
descendants need not be trees themselves - they may be any arbitrary graph. These
descendants thus form a list of graphs and are called branches. However, there is
one restriction - nodes from different branches cannot have links between them. An
example pre-tree is shown in Figure 1. Note that pre-tree is another data structure like
multi-trees [4] - it is not as complex as a graph
but not as simple as a tree. Also note that although the term ``pre-tree'' has not been
used before, this data structure has a long history in top-down clustering techniques
[5]. Top-down clustering would often be halted when new
divisions were not auspicious, leaving a final structure which is essentially a pre-tree.
FIGURE 1:
An example pre-tree. It has a root node which does not have any parent. The
descendants of the root node are graphs. However, none of these graphs have any links
between them. Our hierarchization algorithm tries to identify the best pre-tree to
represent the given graph. The final tree is formed by calling the algorithm recursively
for the branches.
Hierarchization Algorithm
The algorithm tries to identify a suitable pre-tree from a given graph. Thus a root node
is identified and the other nodes are partitioned into branches. This root node forms the
root of the final hierarchy. The algorithm is recursively called for each of the branches
and the trees formed by these recursive calls become children of the root of the final
hierarchy. The recursion stops if a branch has very few nodes or the required depth of the
final tree has been reached. It may also happen that for certain branches, no suitable
pre-trees can be formed. In these cases, the nodes of the branches become children of the
parent of the branch. (This case generally occurs for branches with very few nodes).
For identifying potential pre-trees both content and structural analysis are used.
- Content analysis:
For content analysis, for each attribute, the nodes of the graph are partitioned into
branches based on the attribute values by Content-based Clustering. The
clustering algorithm is explained in [11]. If too many or
too few branches are formed, the attribute is not suitable for forming a pre-tree.
Otherwise a new pre-tree is formed with these branches. The root of the pre-tree is a
cluster representing all the nodes of the graph.
- Structural analysis:
A pre-tree is formed for nodes in the graph which can reach all other nodes. These nodes
are designated as the roots of the pre-trees. The branches are the branches of the
spanning tree formed by doing a breadth-first search from the designated root node. (A
detailed analysis is omitted for the purpose of brevity. The algorithm is explained with
examples in the next section).
Both content and structural analysis can identify several potential pre-trees. A
metric is used to rank these pre-trees. The metric consists of the following
submetrics:
- Information lost in the formation of the pre-tree: When the nodes are partitioned
for forming the branches, all links joining nodes in different branches are removed. Thus
valuable information is lost and a submetric calculates the ratio of the number of links
remaining in the branches to the total number of links in the original graph to rank the
pre-trees in order of the least amount of information lost.
- "Treeness" of the branches: Since our overall objective is to form trees, it is
advantageous if the branches of the pre-tree are already close to trees. If all the
branches only consisted of trees, there would be a total of n - c links where
n is the total number of nodes in the branches and c is the number of
connected components. Thus a submetric which calculates the ratio (n-c)/l
where l is the total number of links is an indication of the "treeness" of the branches.
- "Goodness" of the root: For a structural pre-tree the goodness of the root is
determined by the sum of the distances of the shortest path from the root to all other
nodes. A "good" root will reach all other nodes by following only a few links so that
the resulting tree is not very deep. A deep tree is not desirable since it will force the
user to follow a long and tedious path to reach some information. For content analysis the
goodness of the root is determined by the relevance of the attribute. (For example, for an
automobile database, the manufacturer of the cars is a more relevant attribute than the
number of doors of the cars).
Each submetric returns a number between 0 and 1. The overall metric is calculated by a
weighted sum of the submetrics where the weight is determined by the relative importance
of the submetrics.
The Role of the User
By default, the entire process would be automatically forming the "best" hierarchical
form for the original graph. However, the user can guide the process both during the
translation of the graph to a tree and during the visualization of the tree.
- Translation phase:
- The users can control the various variables that are used in the translation
process. For example, they can control the variable which specifies the maximum possible
depth of the tree (the recursion stops when this depth is reached).
- The user can control the relative importance of the various submetrics in the
overall metric that is used to rank a given pre-tree. For example the user can specify
that the "goodness" of a root is not a useful criteria for judging pre-trees. The user
can also assign different weights to different link types to influence the submetric
calculating the amount of information lost.
- The algorithm generally selects the best possible pre-tree at each level. However,
the user can choose the pre-tree instead. The user is shown the possible pre-trees that
can be selected ranked by the metric and the user can choose one of them. The user can
specify to what level of the hierarchy the pre-trees would be chosen. By choosing
different pre-trees during different runnings of the algorithm, different hierarchies,
giving different perspectives to the data can be formed.
- Visualization phase:
- Besides a 2D tree, the hierarchy can also be visualized as Cone Trees, Treemaps
or as a Table of Contents of a book (which is formed by listing the nodes in the order of
a depth-first search).
- Different visual attributes can be bound to information attributes in the views.
This is an extension of the work reported in [10].
IMPLEMENTATION
The algorithm has been implemented in the Navigational View Builder, a system for forming
overview diagrams of hypermedia systems. Figure 2 represents an overview diagram of an
automobile database. There are a lot of interconnected nodes showing, for example, textual
information about the cars, images of the cars, TV advertisements and audio of previous
buyers' comments. There are also links to other cars with similar price and other models
by the same manufacturer. From this complex network a hierarchy can be formed
automatically. The top-level root of this tree and its children are shown in the left hand
screen of Figure 3. In this case, the attribute Price was used to form the
initial partitioning and the root represents a cluster for all the nodes.
FIGURE 2:
An overview diagram of an automobile database. The diagram is very difficult
to comprehend.
FIGURE 3:
The left hand screen shows the default tree formed for the automobile database. The
top-level partitioning is by the attribute Price. The right hand screen shows
the tree formed if the top-level partitioning is done by the attribute Country.
The user can form different hierarchies by selecting other pre-trees. For example, if the
user wanted to select the pre-tree at the initial level, the dialog box shown in
Figure 4 pops up. If the user wants to partition based on the attribute Country,
the tree shown in the right hand screen in Figure 3 is formed. In this figure some of the
children represents clusters for countries. For example the node labeled Japan represents
all the Japanese cars and its children are shown in the left hand screen of Figure 5. Here
the partitioning is done by the attribute Manufacturer. For some other countries
the nodes in the cluster formed a tree. In these cases the roots of the tree were
identified by structural analysis and they became the children of the overall root. Thus
for Sweden, Saab-Info is the root of the tree for all nodes related to Swedish cars. Its
children are shown in the right hand screen of Figure 5.
FIGURE 4:
At each level various pre-trees can be used. A metric ranks these pre-trees. By default
the pre-tree with the best metric is selected. However, the user can select others using
the above menu.
FIGURE 5:
Examples of Content and Structural analysis for forming pre-trees. The left hand
screen represents the nodes for Japan. The root is a cluster representing all Japanese
cars. The nodes are partitioned by the attribute Manufacturer. The right hand
screen is for Swedish cars. These nodes form a tree with the node Saab-Info as the root.
Figure 6 shows a 3D Tree view of this hierarchy. In this view, the colors of the nodes
represent various countries and the colors of the links represent link types. Various
zooming and filtering operations that are mentioned in
[15] are possible for this 3D tree. Moreover, smooth
animation is used so that the view changes are not abrupt and allow the user to see the
changes easily. (Note that the implementation is done using C++, Motif and Open Inventor
[18].)
FIGURE 6:
A 3d tree View of a hierarchy of the automobile database. Initial partitioning by the
attribute Country. Node colors represent different countries and the link colors
different link types.
Forming Hierarchies in the World-Wide Web
Let us now look at an example from perhaps the most popular hypermedia system, the
World-Wide Web. For input to the Navigational View Builder, information was
automatically extracted from the WWW about the various files, their authors, their links
to other files and other information by parsing the HTML documents using the method
described in [14]. Figure 7 shows an unstructured overview
diagram of the WWW pages about the research activities at the Graphics Visualization
& Usability (GVU) Center at Georgia Tech.
(URL: http/::/www.gatech.edu/gvu/gvutop.html) Obviously, this information is very complicated.
FIGURE 7:
An overview diagram of the World-Wide Web pages about the research activities at GVU. It
indicates clearly why traditional overview diagrams are useless for real-world hypermedia systems.
The left hand screen of Figure 8 shows the top level of the hierarchy automatically
created for the data by the system. The file research.html which lists the
various research activities of the GVU Center is the root. It has branches to the major
research area as well as to gvutop.html, a file containing general information
about GVU. The right hand side of Figure 8 shows a view of a section of this hierarchy
where the nodes are listed as a table of content of a book.
FIGURE 8:
The left hand screen shows the top level of the default hierarchy formed for the
GVU WWW pages. research.html is the root and the major research areas are shown.
The right hand screen shows a book view of a portion of this hierarchy showing research in
Software Visualization.
A major drawback of the World-Wide Web is that very few useful semantic attributes are
defined for the pages. To create some other meaningful hierarchies, attributes like the
topic of the page (whether it is a research page or a personal page, etc.) were inserted
manually. (Efforts are underway to incorporate metadata into WWW and hopefully in the near
future we can extract all useful information from the WWW automatically.) The left hand
screen of Figure 9 represents a treemap view of a hierarchy formed when the initial
partitioning is done by the topic of the page. The colors are used to represent the kind
of users who created the pages. Green is used to represent Phd students and the color
plate indicates that the Phd students are the primary authors of the pages.
FIGURE 9:
The left hand scree shows a Treemap view of a hierarchy of the GVU WWW pages. Initial
partitioning is by the attribute Topic . Colors represent different types of
authors. The selected node is visdebug.html . The corresponding WWW page is
shown on the right.
Multiple hierarchies, each giving a different perspective to the underlying information
space can be formed. If a user selects a node in one view, its positions in the other
views are also highlighted. Thus, these views help the user in comprehending the data. It
should be also noted that the user can go directly to the corresponding WWW page for the
selected node. Thus in the Treemap view, the node visdebug.html is highlighted.
The corresponding WWW page is shown on the right hand screen of Figure 9.
GENERATING OTHER VIEWS
Once a hierarchy is formed from the original graph structure, the hierarchy can be
transformed to other data organizations as well. Visualizations can be formed for these
data organizations also. For example, if the original partitioning for forming the
hierarchy was done by a quantitative attribute, a linear structure sorted by that
attribute can be formed from the subtrees of the root node.
Figure 10 represents a perspective wall [9] view of a
linear arrangement of the GVU WWW pages sorted by the last modification times of the
files. From the hierarchy whose initial partitioning was by the attribute
last-modified-time, the files were divided into partitions based on the time when
they were last modified. These partitions were arranged on walls. Only some walls are in
the focus at a given time. The user can easily control the walls which are in focus
through a scrollbar. Similarly, for the automobile database a Perspective Wall view can be
formed where the cars are sorted by the attribute Price.
FIGURE 10:
A Perspective Wall view showing a linear arrangement of the files based on the last
modification time. The different walls show files which were last modified in different
time frames. Only some walls are in the focus at a given time.
Other views can also be generated. For example, a tabular view showing information like
average price, mileage, etc. for various car models and also such useful statistics for
different manufacturers of the cars can be formed by a depth-first traversal of the
hierarchical structure whose partitionings are done by the attributes
Manufacturer and Car-Model.
RELATED WORK
Our structural analysis is similar to that described in [2]
for identifying hierarchies from hypermedia structures. Although using just structural
analysis to identify hierarchies works for hypertext systems with simpler underlying
structures, identifying meaningful hierarchies by structural analysis alone is difficult
for real-world systems. Content analysis is also essential as is evident from the paper.
[6] describes a method to linearize complex hyper-networked
nodes to facilitate browsing using a book metaphor. However, this work also uses structural analysis only.
This paper is also related to systems that deal with graphical presentation of
information automatically or semi-automatically. Examples include APT
[8] and SAGE [16]. However,
our information domain is different from these systems - these systems deal with highly
structured information. The views that we want to develop are also different. The previous
systems generally produced bar diagrams, scatter plots and such graph views.
CONCLUSION
One of the best ways to comprehend a large complicated information structure is to form
multiple simpler structures each highlighting different aspects of the original
structure. Our work tries to use this philosophy to make a complex hypermedia system
understandable to the user. We believe that by forming various effective views of the
underlying space, we would allow the user to better understand the complex information.
We give examples of the hierarchization process from two complicated hypermedia systems to
illustrate our point. These examples show that our algorithm was able to extract
meaningful hierarchies which gave better insights into the complex information spaces.
Future work is planned along the following directions:
- Visualizing Larger Databases: Although a detailed complexity analysis is
beyond the scope of this paper, it can be shown that the major bottleneck of the algorithm
is the structural analysis to identify roots. [2] uses an
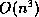 algorithm to identify roots. On the other hand we use
a
algorithm to identify roots. On the other hand we use
a  algorithm to identify roots (by calling the
breadth-first search for each node). Although in the worst case l =
algorithm to identify roots (by calling the
breadth-first search for each node). Although in the worst case l =
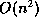 , on average l =
, on average l =
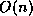 and our algorithm will perform better. For the WWW
database with about 400 nodes and 800 links our algorithm took about 7 seconds on a SGI
reality engine. Although this is acceptable, we will face problems for larger databases.
We are investigating ways to enhance the performance by improving the efficiency of the
code and using probabilistic algorithms to identify roots. Moreover, even cone trees and
treemaps are not able to visualize larger databases effectively. New visualization techniques are needed.
and our algorithm will perform better. For the WWW
database with about 400 nodes and 800 links our algorithm took about 7 seconds on a SGI
reality engine. Although this is acceptable, we will face problems for larger databases.
We are investigating ways to enhance the performance by improving the efficiency of the
code and using probabilistic algorithms to identify roots. Moreover, even cone trees and
treemaps are not able to visualize larger databases effectively. New visualization techniques are needed.
- Usability Studies: A limitation of our system is that no evaluation of how
useful our views really are have been done so far. We plan to do serious usability studies
in the near future. These studies may give us new insights that will help to improve our system.
ACKNOWLEDGEMENT
This work is supported by grants from Digital Equipment Corporation, Bell South
Enterprises, Inc. and Emory University System of Health Care, Atlanta, Georgia as part of
the Hypermedia Interface for Multimedia Databases project. We would also like to thank
the reviewers of this paper for their useful comments.
REFERENCES
- 1
-
G. Battista, P. Eades, R. Tamassia, and I. Tollis.
Algorithms for Drawing Graphs: an Annotated Bibliography.
Technical report, Brown University, June 1993.
- 2
-
R. Botafogo, E. Rivlin, and B. Shneiderman.
Structural Analysis of Hypertexts: Identifying Hierarchies and
Useful Metrics.
ACM Transactions on Office Information Systems, 10(2):142-180,
1992.
- 3
-
K. Fairchild, S. Poltrok, and G. Furnas.
Semnet: Three-dimensional Graphic Representations of Large Knowledge
Bases.
In R. Guindon, editor, Cognitive Science and its Applications
for Human-Computer Interaction. Lawrence Erlbaum, 1988.
- 4
-
G. Furnas and J. Zacks.
Multitrees: Enriching and Reusing Hierarchical Structures.
In Proceedings of the ACM SIGCHI '94 Conference on Human Factors
in Computing Systems, pages 330-336, Boston, Ma, April 1994.
- 5
-
J. Hartigan.
Clustering Algorithms.
John Wiley and Sons, 1975.
- 6
-
S. Ichimura and Y. Matsushita.
Another Dimension to Hypermedia Access.
In Proceedings of Hypertext '93 Conference, pages 63-72,
Seattle, Wa, November 1993.
- 7
-
B. Johnson and B. Shneiderman.
Treemaps: A Space-filling Approach to the Visualization of
Hierarchical Information.
In Proceedings of IEEE Visualization '91 Conference, pages
284-291, San Diego, Ca, October 1991.
- 8
-
J. MacKinlay.
Automating the Design of Graphical Presentation of Relational
Information.
ACM Transactions on Graphics, 5(2):110-141, April 1986.
- 9
-
J. D. Mackinlay, S. Card, and G. Robertson.
Perspective Wall: Detail and Context Smoothly Integrated.
In Proceedings of the ACM SIGCHI '91 Conference on Human Factors
in Computing Systems, pages 173-179, New Orleans, La, April 1991.
- 10
-
S. Mukherjea and J. Foley.
Navigational View Builder: A Tool for Building Navigational Views of
Information Spaces.
In ACM SIGCHI '94 Conference Companion, pages 289-290, Boston,
Ma, April 1994.
- 11
-
S. Mukherjea, J. Foley, and S. Hudson.
Interactive Clustering for Navigating in Hypermedia Systems.
In Proceedings of the ACM European Conference of Hypermedia
Technology, pages 136-144, Edinburgh, Scotland, September 1994.
- 12
-
C. Neuwirth, D. Kauffer, R. Chimera, and G. Terilyn.
The Notes Program: A Hypertext Application for Writing from Source
Texts.
In Proceedings of Hypertext '87 Conference, pages 121-135,
Chapel Hill, NC, November 1987.
- 13
-
H. Parunak.
Hypermedia Topologies and User Navigation.
In Proceedings of Hypertext '89 Conference, pages 43-50,
Pittsburgh, Pa, November 1989.
- 14
-
J. Pitkow and K. Bharat.
WEBVIZ: A Tool for World-Wide Web Access Log Visualization.
In Proceedings of the First International World-Wide Web
Conference, Geneva, Switzerland, May 1994.
- 15
-
G. G. Robertson, J. D. Mackinlay, and S. Card.
Cone Trees: Animated 3D Visualizations of Hierarchical Information.
In Proceedings of the ACM SIGCHI '91 Conference on Human Factors
in Computing Systems, pages 189-194, New Orleans, La, April 1991.
- 16
-
S. Roth, J. Kolojejchick, J. Mattis, and J. Goldstein.
Interactive Graphic Design Using Automatic Presentation Knowledge.
In Proceedings of the ACM SIGCHI '94 Conference on Human Factors
in Computing Systems, pages 112-117, Boston, Ma, April 1994.
- 17
-
K. Utting and N. Yankelovich.
Context and Orientation in Hypermedia Networks.
ACM Transactions on Office Information Systems, 7(1):58-84,
1989.
- 18
-
J. Wernecke.
The Inventor Mentor: Programming Object-Oriented 3D Graphics
with Open Inventor.
Addison-Wesley Publishing Company, 1994.
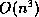 algorithm to identify roots. On the other hand we use
a
algorithm to identify roots. On the other hand we use
a  algorithm to identify roots (by calling the
breadth-first search for each node). Although in the worst case l =
algorithm to identify roots (by calling the
breadth-first search for each node). Although in the worst case l =
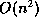 , on average l =
, on average l =
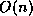 and our algorithm will perform better. For the WWW
database with about 400 nodes and 800 links our algorithm took about 7 seconds on a SGI
reality engine. Although this is acceptable, we will face problems for larger databases.
We are investigating ways to enhance the performance by improving the efficiency of the
code and using probabilistic algorithms to identify roots. Moreover, even cone trees and
treemaps are not able to visualize larger databases effectively. New visualization techniques are needed.
and our algorithm will perform better. For the WWW
database with about 400 nodes and 800 links our algorithm took about 7 seconds on a SGI
reality engine. Although this is acceptable, we will face problems for larger databases.
We are investigating ways to enhance the performance by improving the efficiency of the
code and using probabilistic algorithms to identify roots. Moreover, even cone trees and
treemaps are not able to visualize larger databases effectively. New visualization techniques are needed.