Abstract Data Types

Touretzky Reading: None

This lecture is lifted basically in its entirety from Kurt Eiselt's lecture on this material.

Data Abstraction

We've all become familiar with procedural abstraction... haven't we?!? We are giving you a taste of this with lab 4 and with programming assignment 3.

What does it buy you?

Aids in design, maintainability, adaptability, readability, etc. (Mom and apple pie...)

What is it painful?

Let's face it, we're all used to just hacking up some code (Kurt's phrasing: "Slam-dunking" code) and all this abstraction is hard to think about if we're not used to it. Ugh. We get similar benefits by abstracting away the details of our data structures. We want to be able to write our code in waays that focus on the high-level concepts about the data, while postponing the implementation details.

What do we gain from this?

At least one practical benefit: we get to draw pictures. (Don't laugh here, a great many problems are easier to solve if we think about them pictorialy.)

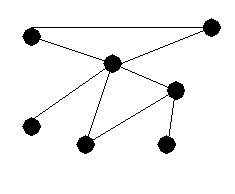
Graphs

There is an abstraction that CS folks us all the time. It's called a graph- which is just a collection of vertices and edges (or "nodes and lines" or "nodes and arcs"). E.g.

There are a variety of classifications of graphs based on certain properties that they have or don't have. An especially interesting property is whether or not the graph has an cycles... but this is the subject of another course on graph theory.

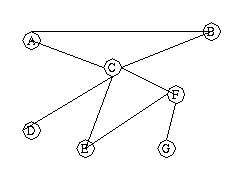
If we want to represent data being contained in the nodes (vertices) of the graph, we'll need to label the nodes: E.g.

If we put orientation on the edges we get a "directed" graph:

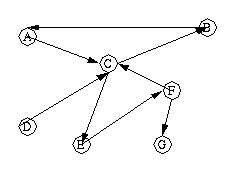
Using (you guessed it) list notation you can represent all of these different structures. These are many of the examples we'll be using in this lecture but you can represent basically any data structure using a list.

Association Lists

Association lists (frequently called "A-lists") are a common Lisp data structure that implements a lookup table or a dictionary. Here is an example of an A-list: ((eiselt 1.9)(shilling 2.2) (greenlee 2.0)) Note that it is organized as a list of sublists. Each element of the main (outer) list is a list of two elements. These two elements are generally called the "key" and "value" for the first and second eleement respectively. You can use the built-in function ASSOC to extract information from an A-List. Consider: > (assoc 'eiselt '((eiselt 1.9)(shilling 2.2)(greenlee 2.0)) ) (EISELT 1.9) > (assoc 'eiselt '((eiselt 1.9)(shilling 2.2)(greenlee 2.0)) :test #'equal) (EISELT 1.9) The first call to ASSOC above uses the predicate EQL (the default) and the second one uses the keyword :test to set its predicate to EQUAL. Beware of not getting what you expect because the built-in ASSOC uses EQL as its test! Note that the value part of the key-value pairs may be anything including a list!

Trees

Suppose we wanted to encode the following special kind of a graph called a tree:

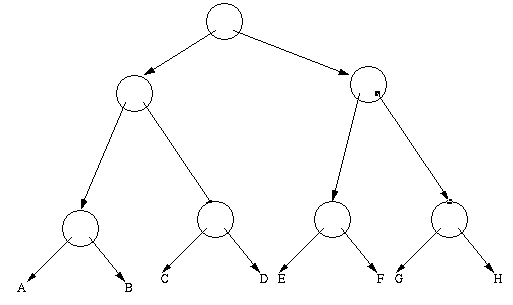
We might use the following Lisp representation if we wanted to encode only the bottommost (leaf) nodes of the tree:

(((a b)(c d))((e f)(g h))) If we had a tree and we wanted to encode all the nodes including the interior (non-leaf) nodes, we might use this lisp representation (a (b (d e))(c (f g))) to encode this tree:

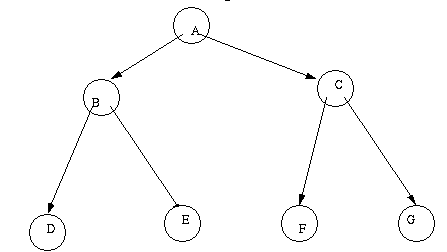
Another equally good representation for this tree might be:

(a (b (d (nil nil) e (nil nil))) (c (f (nil nil) g (nil nil)))) Do you see that a correctly written program might use functions like: get-left-child and get-right-child which could be used to do various manipulations or "walks" of this tree? These functions to get the left and right children could abstract away the details of the implementation (which might be one or the other of the above) and allow you to write your tree manipulation without concern for the implementation.

Another possible encoding of a tree is an A-list. Here is the above tree encoded with an A-list:

((a ( b c)) (b ( d e)) (c ( f g))) Should we add (d NIL) to this list? The answer is: It doesn't matter if we abstract the problem sufficiently. As long there is some code which implements get-left-child and get-right-child it is not important to the higher layers of the software whether we put the (d NIL) in the list or not. We just deal with the get child functions and depend on them to do their job.

So now what happens if you write some big Lisp program, one shows tons of procedural abstraction, but you've written everything that accessses the tree data structure in such a way that it's dependent on the nested list implementation of a tree ... and then some loser (say, your boss) comes along and says, "That tree is too hard to read, I want you to use the A-List version!" You get to rewrite lots of code.

But if you had written the code that treated the tree as a very high-level, abstract object and postponed the details of the implementation to a few low-level acessor functions? You are the big winner!

You can get some measure of the goodness of your program by evaluating how much of the code that deals with the data structures actually depends on implementation details:

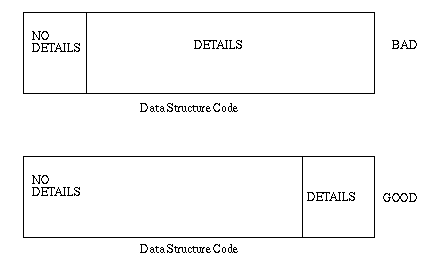
This represents the difference between a program that has used abstraction to effectively postpone the details and one that doesn't...

Back To The CS2360 Home Page
Ian Smith (iansmith@cc.gatech.edu)
Last Modified 5 Feb 95 by Ian Smith (iansmith@cc.gatech.edu)