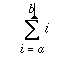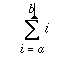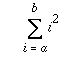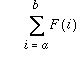Applicative Programming
Touretzky Reading: Chapter 7
Touretzky Exercises: 7.2, 7.4, 7.7, 7.14, 7.16, 7.18, 7.27
Administrivia
- Mobiles (program 2 help):
Applicative Programming
Say you wanted to compute the following:
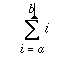
You'd probably code it up like this:
(defun sum (a b)
(cond ((> a b) 0)
(t (+ a (sum (+ a 1) b)))))
But, now say you want to code up this sum:
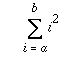
You'd probably want to do something like this:
(defun sum-sq (a b)
(cond ((> a b) 0)
(t (+
(* a a) <--- crucial line
(sum-sq (+ a 1) b)))))
There is a similarity here... all you have to do is change the crucial
line to get different summations. What you really want is to generate
a function which can represent a class of functions like this:
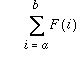
The way to this is to use the FUNCALL function which calls the
function that is its first argument with the parameters that are all
the rest of its arguments. So here is how to code the summation above:
(defun sum-whatever (a b f)
(cond ((> a b) 0)
(t (+
(funcall f a)
(sum-whatever (+ 1 a) b f)))))
Note that sum-whatever defines a class of functions, not just one
functions.
To assign a function to a variable (parameter) you need the function
FUNCTION or its abbreviation #'. For now, you should
think of this as extracting the value associated with a function's
name. E.g:
(function car)
#<Compiled-Function CAR 502DDE>
Thus to call our summation function we would use:
> (sum-whatever 1 100 #'sqrt)
671.4629471031477
This computes the sum of the first 100 square roots.
Note that the FUNCTION function does not only extract
the code associated with a function but also some environment. This is
known as a "lexical closure" and will be discussed in detail later.
MAPCAR
MAPCAR is your friend. MAPCAR is an apllicative
operator which maps a function of your chosing over a set of data of
your chosing. Consider:
> (mapcar #'sqrt '(1 4 9 25))
(1.0 2.0 3.0 5.0)
This applies the function that is its first argument to all the data
provided in the second argument. It produces an element in the output
for each element of the input, and these are in the same
order. Similarly you can use it to do list manipulation:
> (mapcar #'first '((a b) (c d) (e f)))
(A C E)
It will also work for multi-inputted functions if you give it a
sufficient number of inputs. For a two input function, it needs two
lists of data. E.g.:
> (mapcar #'- '(1 2 3) '(4 5 6))
(-3 -3 -3)
If the lists are different lengths, it stops when the shortest list is
exhausted.
Anonymous Functions
The "function" LAMBDA creates anonymous functions. Consider this:
> #'(lambda (n) (* n n))
#<Interpreted-Function (LAMBDA (N) (* N N)) 9E1936>
Note that you can not just "call" LAMBDA:
> (lambda (n) (* n n))
>>Error: The function LAMBDA is undefined
This can be be used to convert a two input function into a one input
function or vice versa.
Note that the evaluation of a lamba expression is a lexical closure.
Example Applicative Operators
> (find-if #'(lambda (x) (= 0 x)) '( 1 2 3 2 0))
0
> (remove-if #'(lambda (x) (= 0 x)) '( 1 2 3 2 0))
(1 2 3 2)
Keyword Operators
Good discussion in 6.14 in Turetzky.
Keywords allow you to pass optional parameters to a function. They
begin with : and they evaluate to themselves.
To use FIND-IF starting from the end instead of the beginning
use:
> (find-if #'oddp '(2 3 4 5 6) :from-end t)
5
You can also control the predicate used for many functions. To make
MEMBER work better for numbers use #'=.
> (member 2.0 '( 1 2 3 4) :test #'=)
(2 3 4)
> (member 2.0 '(1 2 3 4))
NIL
Scoping & Lexical Closures
Consider this function:
(defun my-assoc (key table)
(find-if #'(lambda (entry) (equal key (first entry))) table))
What is passed to the FIND-IF is a lexical closure- not really
a "function" but a "function plus environment." The closure includes
all the necessary information for the function to be evaluated.
Lexical closures carry their creating context with them.
Here is a good example of scoping and lexical closures:
(defun foo (bar)
(grok #'(lambda (frip)
(+ bar frip)) 3))
(defun grok (fn bar)
(funcall fn bar))
What does (foo 6) evaluate to? It is:
> (foo 6)
9
This shows the lexical scoping in Lisp. Had this been dynamically
scoped (and this is possible in Lisp) you would have gotten:
> (foo 6)
6
You need to always remember that lexical closures carry their lexical
environment around with them. Here is an example of what could happen
if you didn't:
(defun bogus (x)
(+ y x))
(defun bogus2 (y)
(mapcar #'bogus '(1 2 3)))
> (bogus2 10)
>>Error: The symbol Y has no global value
Generators (Digression)
What does this function do?
(defun make-tester (n)
#'(lambda (x) (= x n)))
It creates an equality predicate for numbers based on the value of the
variable n. Here's some examples using it:
> (make-tester 7)
#
> (find-if (make-tester 7) '(8 9 10))
NIL
> (find-if (make-tester 7) '(7 8 9 10))
7
Consider the lexical scoping issues here! When might this type of
function be useful?
What does all this lexical scoping and generator stuff tell about what
DEFUN does?
Apply
> (apply #'+ '(1 2))
3
> (apply #'cons '(x nil))
(X)
>
This is another version of function invocation, but much more useful
when you don't know the arguments you want to pass (or their number)
in advance. Use APPLY when you don't know the arguments in
advance, and FUNCALL when you do.
Be sure to note that the arguments to the function called by
APPLY are not evaluated twice!
Reduce
Takes a two input function and a list and produces an atom that
combines all the elements of the list.
> (reduce #'+ '( 1 1 23 34))
59
It can be surprisingly useful for list manipulation. Here's a
really small way to do selection sort:
(defun largest (input-list)
(reduce #'(lambda (x y) (if (> x y) x y)) input-list))
(defun sorter (input-list)
(cond ((null input-list) nil)
(t (cons (largest input-list)
(sorter (remove (largest input-list) input-list))))))
Back To The CS2360 Home Page
Ian Smith (iansmith@cc.gatech.edu)
Last Modified 19 Jan 95 by Ian Smith (iansmith@cc.gatech.edu)