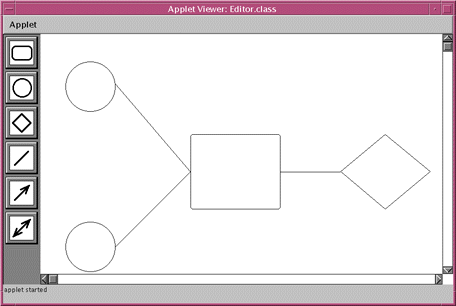
Figure 1. Simple Interface Requiring Both Top-Down and Bottom-Up Layout Strategies

ALGORITHMIC BACKGROUND
Layout is the process of sizing and positioning objects that appear in a
user interface display. In most modern toolkits, interactive objects (or
simply interactors) are organized hierarchically with a parent object grouping
together a series of subordinate child objects, which may in turn serve
as a parent object, and so on recursively. In a hierarchical setting, most
layout computations can be seen as either bottom-up - where child characteristics
(e.g., size) determine parent characteristics - local - where characteristics
are derived from the object itself or its siblings - or top-down - where
child characteristics are determined by those of the parent (these layout
strategies can also be thought of as inside-out, local, and outside-in respectively).
Each of these basic forms of layout can be carried out within a simple bottom-up
or top-down pass over the interactor tree. Unfortunately, used alone, none
of these forms of layout is typically sufficient. For example, Figure 1
shows a simple interface built with our system which requires several layout
strategies simultaneously. Here we can see that even within a single object,
such as the column object organizing the palette on the left, both bottom-up
and top-down layouts may be needed. In this case the width of the palette
is determined by the size of the buttons within it, while the height expands
to fill the space provided by the parent object.
As a result, although some systems use a single top-down or bottom-up strategy
(for example [5]), most must use a more complex multi-pass strategy. For
example the Xt toolkit [26] uses a very complex negotiation process which
can in the worst case take O(n2) time.
Rather than use a fixed structure of passes over the interactor tree, constraint-based
layout typically allows each of the overall layout strategies to be employed
wherever it is needed. Specific layout computations are then done in an
order that matches whatever specification is made. This order is a dependency-based
order. If a value A needs some value B in order to be computed, we say that
A is dependent on B, and insure that B is computed before A.
Local propagation-based constraint update algorithms typically use a dependency
graph to internally express the dependencies between various values that
control a layout (i.e., values that store the position and size of each
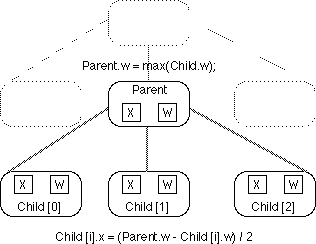
interactor object). If a constraint such as x = (parent.w - w)/2 is declared
in a system, the one-way constraint algorithms used in this paper would
establish dependency edges from the attributes parent.w and w to the attribute
x as shown in Figure 2. This indicates that information flows from parent.w
and w to x and hence x must be computed after they have been given valid
values. (In contrast a multi-way algorithm would typically begin with a
related undirected graph, then in a planning step choose a direction for
each edge, after which the resulting one-way problem would typically be
solved whenever parent.w or w were changed.)

The constraint evaluation algorithm used in the work described here is
a simple, but relatively efficient one. It is a simplification of the lazy
update algorithm described in [17]. It works in two phases: when attribute
values change (for example, when an object's size changes or it is reparented),
any attributes which are directly or indirectly dependent upon the changed
values are marked as out-of-date. These attributes are found by simply traversing
the dependency graph forwards from the point(s) of change, marking all reachable
attributes. Whenever an attribute value is requested, its out-of-date mark
is examined. If the attribute is marked, then it may be out of date with
respect to its defining equation and an evaluation of its constraint is
done. This evaluation removes the out-of-date mark , recursively requests
any attribute values needed to compute the constraint, and then executes
the function associated with the constraint to obtain a new value. Attributes
which are not directly or indirectly requested remain out-of-date until
they are needed (hence this is a lazy update algorithm).
This algorithm, although not optimal (it does not do the early quiescence
or non-strict function optimizations found in [17]), is fairly efficient,
and has the property that it only requires one bit of bookkeeping information
for each attribute (for the out-of-date mark). It also shares a property
with essentially all other update algorithms: it must traverse portions
of the dependency graph both forwards and backwards. The dependency graph
is traversed forwards in the mark out-of-date phase and backwards during
the evaluation phase. As a result, a straightforward implementation of the
algorithm would need to keep dependency edge pointers in both directions
(in data flow terms both the outgoing and incoming edges). Storage of these
dependency edges is one of the larger uses of bookkeeping space and elimination
of this storage is key to the result presented here. Note that while the
set of incoming edges is bounded by the number of values mentioned in the
constraint equation, the number of outgoing edges is not bounded. As a result,
more expensive variable sized data structures are typically needed if constraints
can be attached and detached dynamically.
µCONSTRAINTS
In order to minimize the space used for constraint bookkeeping, several
important observations can be made. First, since they are only used during
actual evaluation and do not change unless the constraint changes, incoming
dependency edges can be implicitly maintained within the code used for constraint
function evaluation and do not need to be explicitly stored (this approach
is also taken in several other existing systems including [18]). Second,
for layout constraints, the vast majority of constraints reference only
the local neighborhood of an object, that is the parent, children, or siblings
of an object. As a result, most outgoing dependency edges go only to attributes
in this local neighborhood. Further, regardless of the use of constraints,
a typical toolkit must maintain data structures that allow access to these
same parent child, and sibling objects. Finally, we can note that many layout
constraints come from a small set of operations, most commonly equality
or copy constraints, and constant offset constraints (which typically place
objects a fixed distance apart or with a fixed margin).
Using these observations, we can create a limited form of constraint that
does not need to store any dependency edges. It does this by limiting its
domain to the local neighborhood of a given object (specifically, itself,
its parent, its children, and it next and previous sibling), by taking all
constraints from a limited set, and by dynamically inferring the existence
of the edges as needed.
Each constraint from the limited set implies a particular set of incoming
dependency edges, and as in other systems, these are not explicitly stored.
The key to the µconstraint technique involves outgoing dependency edges.
When operations need to traverse outgoing edges - in the case of the algorithm
used here to propagate an out-of-date mark - each of the potentially dependent
neighbor attributes is consulted. Each attribute in turn consults the constraint
attached to it to determine which incoming dependency edges are implied
by the constraint. If an incoming edge from the inquiring attribute is implied,
then the corresponding outgoing edge also exists, and the operation across
that edge (i.e., marking out-of-date) is performed. Otherwise, the operation
is simply ignored.
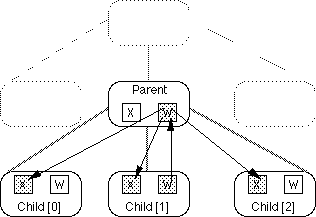
Figure 3 illustrates an example of this process. Figure 3(a) shows part
of an interactor hierarchy and the constraint equations applied to it. In
this case we have constraints suitable for a centered column layout. Each
child object centers itself horizontally with respect to the parent object,
and the parent sets its width to cover the maximum width of its children.
(The subArctic toolkit in fact supplies a column interactor which applies
exactly these constraints). Note that no dependency edges are stored, only
an encoding of the constraint equations.
Let us suppose that the width of child[1] changes. In response to this,
the µconstraint system needs to infer the outgoing edges from child[1].w
and mark all other attributes that directly or indirectly depend on it out-of-date.
To do this, it attempts to propagate out-of-date marks to all neighbors
of child[1] - in this case, parent, child[0] and child[2]. The constraint
attached to each horizontally oriented attribute belonging to those objects
is consulted to determine if there is an implicit incoming edge from child[1].w
to that attribute. In this case, none of the sibling attributes have an
implied incoming edge, so the mark out-of-date operation for them is ignored.
However, parent.w depends upon the widths of all of its children so an edge
from child[1].w to parent.w is inferred and parent.w is marked out-of-date.
Marking parent.w out-of-date causes additional out-of-date marks to be propagated.
Again, out-of-date propagation is attempted for all the neighboring objects.
In this case, the child objects each have a constraint which implies an
edge from parent.w to child[i].x. Consequently each of these attributes
is marked out-of-date, while other objects ignore the out-of-date propagation.
Figure 3(b) shows the dependency edges that were inferred by this process
along with final out-of-date marks.
This scheme represents a speed for space tradeoff. We use an indirect encoding
scheme which requires polling a small set of local neighbors in order to
avoid storage of dependency edges. This increases run-time by consulting
attributes which are not actually dependents during the mark out-of-date
phase of the algorithm. This does not change worst case behavior of the
algorithm (which is still bounded by O(N+E) where N is the number of attributes
and E is the number of dependency edges). However, it can reduce the savings
normally gained by incremental update in some cases (particularly when large
numbers of children must be consulted). Based on our performance tests (below)
and experience with the system thus far, we believe this tradeoff is a good
one.
CONSTRAINT ENCODING DETAILS
An implementation of the µconstraint approach has been constructed
within subArctic (the Advanced Reusable Constraint-oriented Toolkit for
Interface Construction - Subset), an experimental new toolkit written in
Java (this toolkit is a successor to the Artkit toolkit described in [10,
19]).
The subArctic implementation of µconstraints encode constraints in
16 bits and use two additional bits of bookkeeping per constraint. There
are four layout attributes per object: x, y, width, and height resulting
in a total overhead for layout constraints of 9 bytes per object .
Each constraint in this system either comes from a fixed set of 6 functions
(listed below), or invokes a "hook" to use a conventional heavyweight
constraint. Further, each constraint is limited to referring to one or two
other attributes within its local neighborhood plus in some cases a fixed
attribute of itself. Within these limitations, each constraint is encoded
in four parts as indicated below:
The object depended upon (3 bits)
Constraints may refer to one of: self, parent, previous sibling, next sibling,
first child, last child, maximum child, or minimum child.
The attribute within that object (2 bits)
Attributes can only refer to other attributes having the same orientation
(i.e., x and width may not depend upon y or height). Each attribute may
depend on one component of the selected object. It may depend on the top
or left, the bottom or right, the width or height, or the horizontal or
vertical center of the object. The bottom, right, and center components
of an object are implicitly computed from the x or y position and the width
or height of the object in question. Choice of a minimum or maximum child
is done based on the values of the selected attribute compared across all
child objects.
If the position of a non-existent sibling is requested the value corresponding
to the edge of the parent found in that direction is returned instead. Finally,
zero is substituted for the size of a non-existent sibling or when min or
max is taken over an empty child list.
A constant parameter (8 bits)
Each constraint function is provided with an 8 bit unsigned parameter value
(listed as "parm" in Table 1).
A function selector (3 bits)
Each function (except "none" and "external") operates
over the value selected by the encoding described above (denoted as "value"
in Table 1) as well as an 8 bit constant parameter value (denoted as "parm").
The available functions and their meaning are shown in Table 1. Note that
several functions include implicit parameters. These include the width or
height of the object being constrained (as denoted by "wh") and
the x or y position of the next sibling (as denoted by "next_sibling.xy").
Like many modern toolkits, the subArctic toolkit uses hierarchical coordinates
where each object introduces a new coordinate system with its top-left corner
at 0,0. To make best use of hierarchical coordinates, position values are
transformed before use in constraint equations (width and height values
are coordinate system independent and hence are not transformed).
Each position value from a parent or sibling is transformed to be in the
coordinate system of the parent of the object being constrained (the same
coordinate system that the x, y position of that object is expressed in).
As a result, the parent.left and parent.top values are always zero. Each
position value from a child object is transformed into the coordinate system
of the constrained object. Because of the hierarchical coordinates which
place the constrained object's top left at 0,0, this allows the positions
of child objects to be safely used to compute the size of the parent object
(e.g., the width of a parent can be derived from the right edge of the last
child as expressed in the parent's coordinate system).
Finally, note that the "none" and "external" evaluation
functions ignore the attribute encoding of the first part of the constraint
and do not request a value. The "none" function is used to denote
that the attribute in question is not constrained. This is required since
the 16 bit constraint encoding is always present.
The "external" function represents a "hook" for invoking
an externally defined constraint when the µconstraint system is not
expressive enough. When this value is coded, the object refers to a global
hash table to find a constraint object associated with the interactor and
attribute in question. This heavyweight constraint may refer to any values
and may use any constraint function the user wishes to code. This allows
attributes to be "bridged" across neighborhood boundaries and
also provides a convenient interface to allow application objects to be
connected to the layout constraints.
| Name | Equation | Use |
|---|---|---|
| plus_offset | value+parm | Positive offset from another value |
| minus_offset | value-parm | Negative offset from another value |
| centered | (value-wh)/2+parm | Typically used with parent.wh to perform centering |
| plus_far_off | value-wh+parm | Positive offset from the right or bottom edge |
| minus_far_of | value-wh-parm | Negative offset from the right or bottom edge |
| fill | next_sibling.xy - value - parm | Distance from given position to left or top of next sibling |
| external | -- | Constraint is an "external" (heavyweight) constraint |
| none | -- | No constraint is applied to the attribute |
In addition to the 16 bit constraint encoding, two other bits are stored
for each attribute in the subArctic implementation. One bit is used for
the out-of-date mark associated with the attribute. The second bit indicates
whether there are any external constraints that depend upon the attribute
(i.e., whether there are outgoing edges from this attribute to an external
constraint). Whenever an attribute is marked as out-of-date, this bit is
consulted. If it indicates the existence of external outgoing edges, a global
hash table that maintains external edge lists is consulted, and out-of-date
marks are propagated to each attribute or external object found there. Note
that this bit represents a speed optimization and is not strictly necessary
since the hash table could simply be consulted on every mark out-of-date
operation.
EXTENSIONS
The subArctic implementation of µconstraints was designed to explore
the question of how small constraints could be and still cover nearly all
cases needed for layout. There are also several other possible techniques
not currently implemented by the system (some requiring additional space)
that could be applied to increase the functionality of µconstraints.
First, since the "none" and "external" functions do
not use the encoding for a dependent value or parameter, the encoding for
these functions is redundant (i.e., 13 bits are unused). By recognizing
these functions in only one encoded form (e.g., with the remaining 13 bits
set to zero), this would leave 16,382 constraint encodings unused. These
additional encodings could be used with a table of application specific
constraints and/or a table of application specific indirect attributes to
extend the functionality of the system with little additional space or time
cost.
In addition, it is possible to use conventional subclass specialization
to create objects which have a custom set of evaluation functions, replacing
any or all of the six standard functions with other specialized computations.
For example, the standard evaluation functions cannot directly implement
the boxes-and-glue model employed for layout in the Interviews toolkit [22,
23]. However, it would be a relatively simple matter to create an interactor
subclass which changed the interpretation of the three function encoding
bits in order to implement the constraints needed for boxes-and-glue layout.
Furthermore, by using a small amount of additional space for encoding constraints,
it is clearly possible to expand the set of things that can be expressed.
Although in practice we have found that the functions provided cover most
layout constraint needs, adding one additional bit per constraint would
allow twice as many functions to be expressed. Similarly, by adding 5 additional
bits per constraint, it would be possible to support functions over two
dependent attributes rather than just one. This is analogous to two address
machine language instructions, and in general, a compact machine instruction
style of encoding, with mixtures of single and multiple address instructions,
could be employed if more bits were used for constraint encodings.
Finally, it is important to point out that it may be possible to use the
basic µconstraint technique to support other forms of constraints,
in particular to support eagerly evaluated one-way constraints, or even
multi-way constraints. This is because the central technique of avoiding
dependency edge storage can be applied essentially regardless of the update
algorithm. The only real questions for these other algorithms will regard
how small the other bookkeeping used by the algorithm can be made.
PERFORMANCE
In order to test the runtime performance of our µconstraint implementation,
a small benchmark was constructed. This benchmark creates a long chain of
interactor objects whose x position is each constrained to be 20 pixels
to the right of its previous sibling's x position. Similar benchmarks have
been used for other systems (see for example [17, 18, 28, 34]). (Note that
the subArctic implementation of µconstraints has not yet been optimized
for runtime performance.)
1 parent = new min_parent_interactor(0,0);
2 for (int i = 0; i < 1000; i++)
3 {
4 child = new bench_interactor(10,10);
5 if (i != 0)
6 child.set_x_constraint(new constraint(PREV_SIBLING,LEFT,PLUS_OFFSET,20));
7 parent.add_child(child);
8 }