Project 3: Camera Calibration and Fundamental Matrix Estimation with RANSAC
This project is split into three parts. For the first part, we are to calibrate the intrinsic matrix of a camera using the world coordinates and their corresponding projected coordinates, and then estimating the camera center. For the second part, we are given pairs of correspondences in two images from which we can calibrate the fundamental matrix using the 8-point algorithm. For graduate credit, I implemented the normalized 8-point algorithm that recenters the data at the origin and then downscaling the data so that its mean distance from the origin is ~1.414, from which we recover the original fundamental matrix by multiplying the transformed fundamental matrix by the transformation matrix. For the third part, we implement the 8-point algorithm using RANSAC that randomly samples 8 pairs of correspondences and finds the fundamental matrix that leads to the most number of inliers. The implementations involved in the second and third parts are then tested using the images provided in the data, and results will be subsequently discussed.
The following functions are implemented in this project, and are listed below along with brief descriptions.- calculate_projection_matrix.m: This function computes the camera intrinsic matrix corresponding to the input world and projected coordinates.
- compute_camera_center.m: This function computes the camera center for the particular camera used to generate the projected coordinates.
- proj3_part1.m: Runs the two functions above to help in debugging, and provides a visualization of the projection and camera center.
- estimate_fundamental_matrix.m: This function calculates the fundamental matrix using the corresponding pairs of matches via the 8-point algorithm.
- proj3_part2.m: Runs the function above and generates equipolar lines to see if the fundamental matrix is calculated correctly.
- ransac_fundamental_matrix.m: Randomly samples 8 points for which generate a sample F_matrix (fundamental matrix), and choose the best F_matrix which has the largest no. of inliers. This is repeated over an arbitrary number of iterations and stops when a satisfactory fundamental matrix is found.
- proj3_part3.m: Runs the function above on three different pairs of images and visualizes the matching features on each pair.
Code for Normalized 8-point algorithm
Since the non-normalized version of the 8-point algorithm occassionally lead to poor numerical conditioning, an normalized version is implemented instead. In the normalized version, the datapoints in each of the pair of matches are first recentered at the origin, and then scaled so that they are on average a distance of 1.414 away (isotropic scaling) from the origin. Then, denoting this transformation by T_a and T_b (one for each of the pair), we can then calculate F=T_b^t*F_transformed*T_a.
function [ F_matrix ] = estimate_fundamental_matrix(Points_a,Points_b)
s=size(Points_a);
noPoints=s(1,1);
transformed_Points_a=zeros(noPoints,3); transformed_Points_a(:,3)=1;
transformed_Points_b=zeros(noPoints,3); transformed_Points_b(:,3)=1;
%normalization
%Step1: translation to center at origin
meanX_a=0; meanX_b=0;
meanY_a=0; meanY_b=0;
for i=1:noPoints
meanX_a=meanX_a+Points_a(i,1);
meanY_a=meanY_a+Points_a(i,2);
meanX_b=meanX_b+Points_b(i,1);
meanY_b=meanY_b+Points_b(i,2);
end
meanX_a=meanX_a/noPoints; t_ax=-meanX_a;
meanY_a=meanY_a/noPoints; t_ay=-meanY_a;
meanX_b=meanX_b/noPoints; t_bx=-meanX_b;
meanY_b=meanY_b/noPoints; t_by=-meanY_b;
transformed_Points_a(:,1)=Points_a(:,1)-meanX_a;
transformed_Points_a(:,2)=Points_a(:,2)-meanY_a;
transformed_Points_b(:,1)=Points_b(:,1)-meanX_b;
transformed_Points_b(:,2)=Points_b(:,2)-meanY_b;
%Step2 isotropic scaling
s_a=0; s_b=0;
for i=1:noPoints
s_a=s_a+sqrt(transformed_Points_a(i,1)^2+transformed_Points_a(i,2)^2);
s_b=s_b+sqrt(transformed_Points_b(i,1)^2+transformed_Points_b(i,2)^2);
end
s_a=1/(noPoints*sqrt(2))*s_a;
s_b=1/(noPoints*sqrt(2))*s_b;
for i=1:noPoints
transformed_Points_a(i,1:2)=1/s_a*transformed_Points_a(i,1:2);
transformed_Points_b(i,1:2)=1/s_b*transformed_Points_b(i,1:2);
end
%Transformation matrix
T_a=[1/s_a,0,1/s_a*t_ax;0,1/s_a,1/s_a*t_ay;0,0,1];
T_b=[1/s_b,0,1/s_b*t_bx;0,1/s_b,1/s_b*t_by;0,0,1];
%check mean and mean-distance of transformed points
%scatter(transformed_Points_a(:,1),transformed_Points_a(:,2))
%sum=0;
%for i=1:noPoints
% sum=sum+norm(transformed_Points_a(i,1:2));
%end
%sum=1/noPoints*sum
%mean(transformed_Points_b)
A=zeros(noPoints,9);
for i=1:noPoints
A(i,1)=transformed_Points_a(i,1)*transformed_Points_b(i,1);
A(i,2)=transformed_Points_a(i,1)*transformed_Points_b(i,2);
A(i,3)=transformed_Points_a(i,1);
A(i,4)=transformed_Points_a(i,2)*transformed_Points_b(i,1);
A(i,5)=transformed_Points_a(i,2)*transformed_Points_b(i,2);
A(i,6)=transformed_Points_a(i,2);
A(i,7)=transformed_Points_b(i,1);
A(i,8)=transformed_Points_b(i,2);
A(i,9)=1;
end
[U,S,V]=svd(A);
F=V(:,end);
F=reshape(F,[],3);
[U,S,V]=svd(F);
S(3,3)=0;
F_scaled=U*S*V';
F_scaled=F_scaled.*(1/F_scaled(3,3));
F_matrix=transpose(T_b)*F_scaled*T_a;
end
Results
There are two parameters in our RANSAC algorithm that can be altered. One is the no. iterations for which RANSAC is ran, and the other is the conditioning on the value of Af, which should be close to zero. In general, 1000-2000 iterations would be sufficient to generate the F_matrix with the most number of inliers.
The results are listed below. Note that except for the Gaudi pair, the normalized 8-point algorithm does not lead to visibly more pleasing results. The second last set of images corresponds to the Gaudi pair withtout normalization, while the last set of images is the Gaudi pair matched using normalized 8-point algorithm.


|

|


|
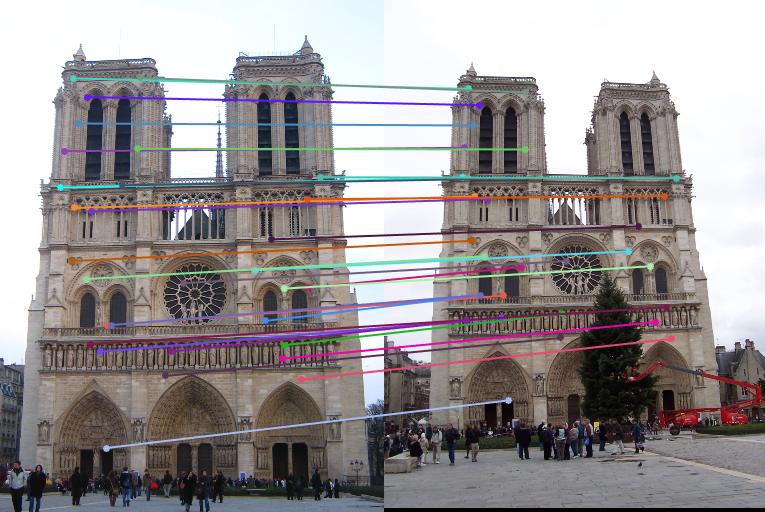
|


|

|


|

|
Extra Credit
I implemented the normalized 8-point algorithm (with isotropic scaling) for graduate credit. For extra credit, I further explored around with different types of scaling, such as anisotropic scaling and non-isotropic scaling. The former leads to no visible differences in results, since the feature matches in each of the three images do not exhibit anisotropy (can be verified by drawing the scatter plot).
The latter was discussed in the paper "In Defence of the 8-point Algorithm", where datapoints are scaled to a circular cloud around the origin, as was done in the figure below.
