Project 3 / Camera Calibration and Fundamental Matrix Estimation with RANSAC
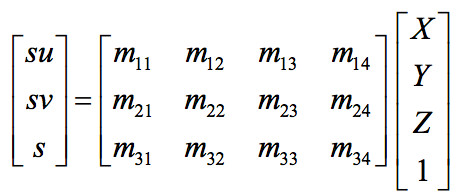
Figure 1
Part I
Part I was about estimating the projection matrix and finding the center of the camera given a set of 2D coordinates and their corresponding 3D coordinates. The projection matrix maps from 3D world coordinates to 2D image coordinates as formulated in figure 1. Z, Y, Z are world coordinates, u and v are image coordinates, and M is the projection matrix. To solve for the projection matrix, we set up the inputs as part of a homogenous linear system as shown in figure 2 and solve for the projection matrix using Singular Value Decomposition where the projection matrix should be the resulting V matrix of SVD.
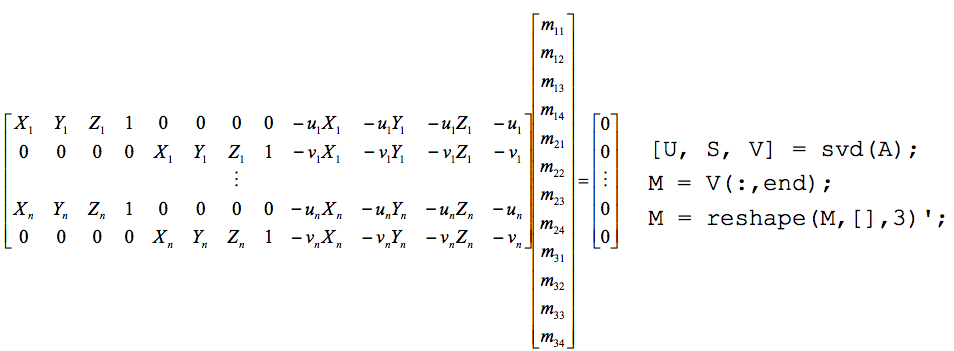
Figure 2
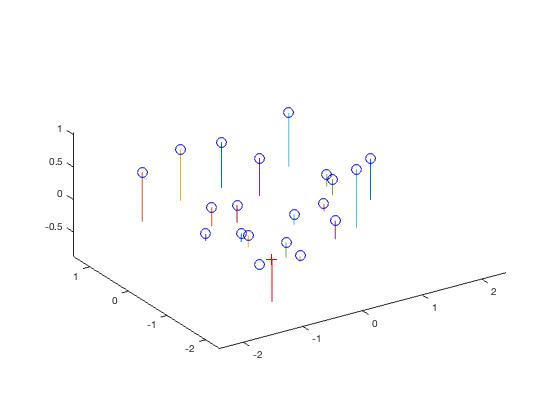
The values for the camera center is captured by the projection matrix, M, which could also be expressed as K[R T]. To find the camera coordinates we need to invert the rotation R and invert the intrinsic parameters K against T. By treating the first three columns of M as K * R and the fourth column of M as T * K, we can calculate the camera parameters as -Q^-1 * m4, where Q and m4 are the first three columns and last column of M respectively.
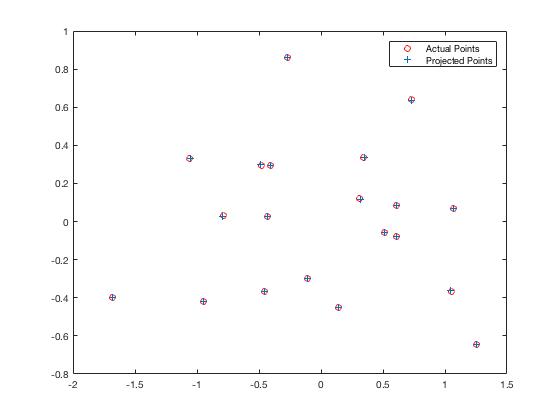
The results gave a residual of about 0.0445 and <-1.5127, -2.3517, 0.2826> as the camera center. The projection matrix is given below.
The projection matrix is:
-0.4583 0.2947 0.0140 -0.0040
0.0509 0.0546 0.5411 0.0524
-0.1090 -0.1783 0.0443 -0.5968
Part II
Part II was to estimate the Fundamental Matrix given coordinate mappings between two images. The inputs and be expressed in the formula shown in figure 3, where (u, v) are coordinates of image 1, (u', v') are coordinates of image 2, and F is the Fundamental Matrix. We solve the system for F by using the 8-Point algorithm. First we setup the equation as shown in figure 4, then we solve using Singular Value Decomposition like in Part I.
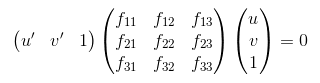
Figure 3
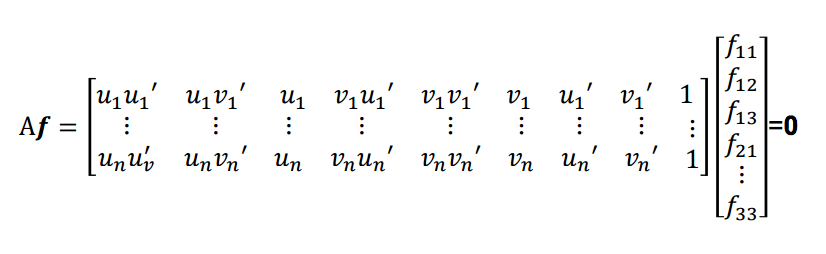
Figure 4
The resulting Fundamental Matrix was shown below. The resulting epipolar lines go straight through the intended coordinates.
F_matrix =
-0.0000 0.0000 -0.0019
0.0000 0.0000 0.0172
-0.0009 -0.0264 0.9995


Part III
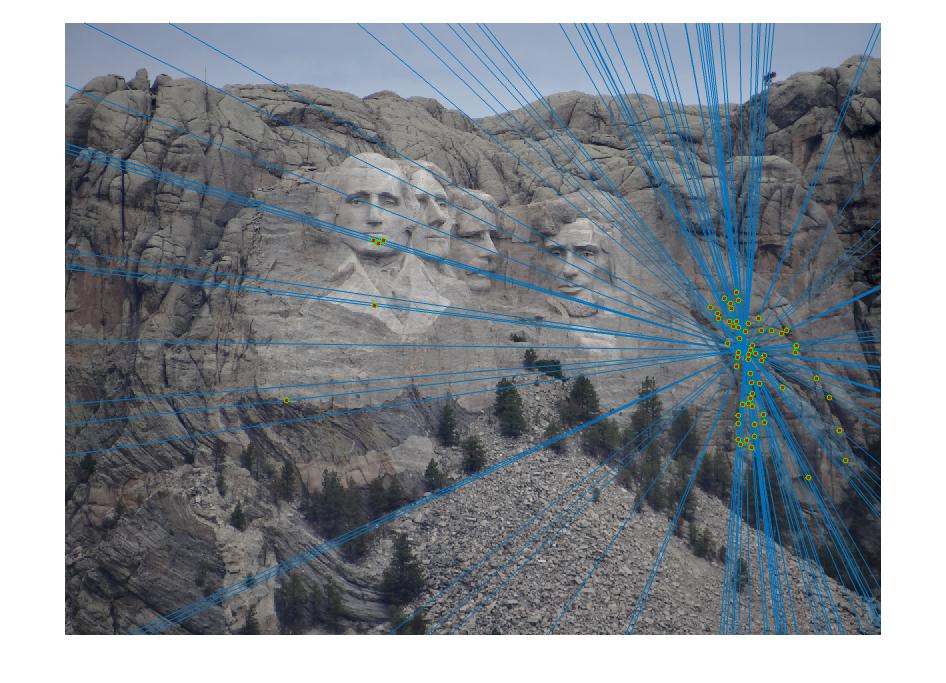
Part III was to estimate the Fundamental Matrix using RANSAC, where the given image coordinates were obtained by SIFT matching and not guarenteed to be accurate. For this implementation of RANSAC, we chose a sample size of 8, and iteration number of 10000, and a matching error threshold of .1%.
Mount Rushmore Results


Notre Dame Results



Gaudi Results



Woodruff Results


