Computer Vision Project

Part I: Camera Projection Matrix

Here, we estimate the camera projection matrix, which maps 3D world coordinates to image coordinates.
Using homogeneous coordinates, the equation for moving from 3D world to 2D camera coordinates is:

We write this equation in the form Am = 0, and solve for 'm' using linear least squares.

M gives the camera projection matrix. Once we have the projection matrix, it is easy to find the matrix K and the matric [R|T] of extrinsic parameters, such as the camera center in world coordinates.
We know that M = (Q|m₄)
The center of the camera can be found by simply computing C = -Q^-1m₄
The following results are obtained for the given normalized 3D coordinates:

The figures below show the estimated 3D location of the camera with respect to the normalized 3d point coordinates:

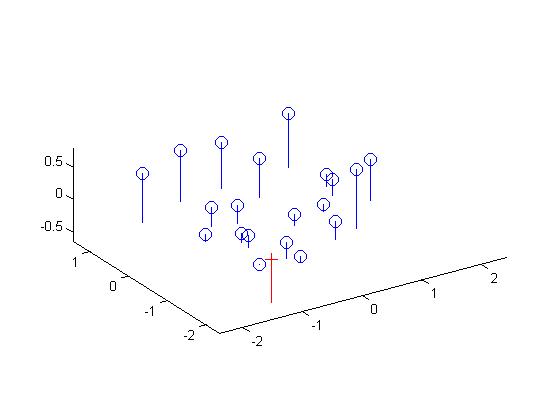
Now, computing the projection matrix and camera centers for the given 3D points without normalization:

The figures below show the estimated 3D location of the camera with respect to the normalized 3d point coordinates:

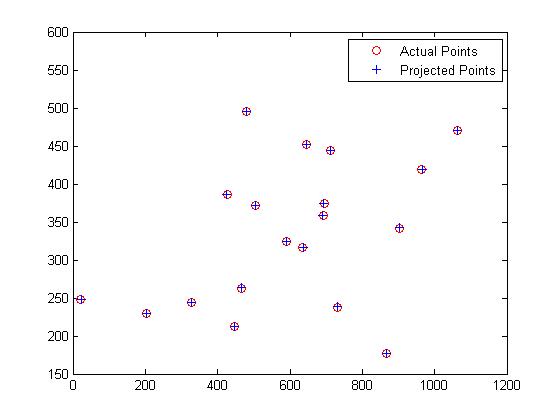
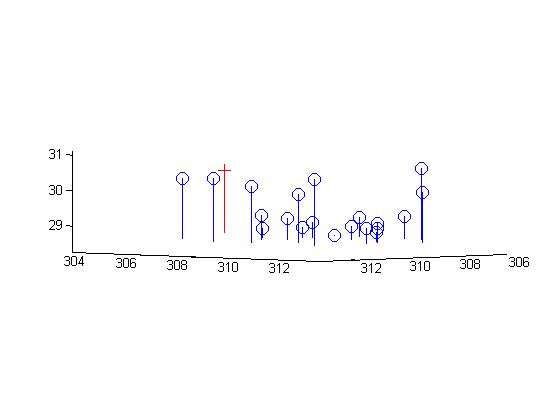
Part II: Fundamental Matrix Estimation

Here, we map points in one image to lines in another by means of the fundamental matrix. We know that the fundamenta matrix is given by:

This can be written in the form Af = 0, as given below:

To solve for f, as in the case of the projection matrix, we perform least squares estimate. However, the least squares estimate of f is full rank, while the fundamental matrix F is a rank 2 matrix. Therefore, we need to reduce the rank. To do this, we decompose F using singular value decomposition into the matrices U, S and V such that F = USV', where S is a matrix of eigenvalues. We then estimate a rank 2 matrix by setting the smallest eigenvalue in S to zero, thus generating S₂. F is then recomputed as US₂V'.

Part II: Extra Credit - Normalizing coordinates

Estimation of the fundamental matrix can be improved by normalizing the coordinates before computing the fundamental matrix. The method mentioned above is standard, but if applied naively it's quite unstable. In real world images, the source and target coordinates are usually noisy, and could have large variance. A simple solution would be to normalize the image coordinates before estimating the fundamental matrix. This provides a very well balanced matrix A (if using the least squares estimate) and a much more stable and accurate results for the fundamental matrix F.


%Function to normalize coordinates:
function [X, T ] = normalize(x)

n = size(x,1);

C = mean(x);
%Subtract means
x_new(:,1) = x(:,1) - C(1);
x_new(:,2) = x(:,2) - C(2);

%Compute standard deviation for mean shifted data
s_u = 1/std(x_new(:,1));
s_v = 1/std(x_new(:,2));

%Transformation matrix
%T = scale matrix x offset matrix
T = [s_u 0 0; 0 s_v 0; 0 0 1] * [1 0 -C(1); 0 1 -C(2); 0 0 1];

% Normalized coordinates
X = (T * [x ones(n,1)]')';
end

...

% Compute Fundamental matrix
F_matrix = T2' * F_norm * T1;

We test the fundamental matrix estimate by drawing the epipolar lines on one image which correspond toa point in the other image. The fundamental matrix is found to be:
Fmatrix =

The epipolar lines are shown in the figures below:

Part III: Fundamental Matrix with RANSAC

Here, point correspondences for 2 photographs of a scene are computed using SIFT.However, these point correspondences are very unreliable. Therefore, to compute the fundamental matrix from this noisy data, we use RANSAC in conjunction with the fundamental matrix estimation to filter away spurious matches and achieve near perfect point correspondence.
The algorithm used is given below:

Values used:
p = 0.99
threshold = 0.05
Maximum no. of Trials = 4000

Results

Mount Rushmore

Inlier Keypoint correspondence:

Epipolar lines:

Notre Dame

Inlier Keypoint correspondence:

Epipolar lines:

Episcopal Gaudi

Without normalized coordinates

The episcopal Gaudi image pair doesn't produce many correct matches unless the comparision is performed at high resolution. This would result in tens of thousands of SIFT features, and time to process these features would be large. We see here that the keypoint correspondences found are very poor (they consist of largely spurious matches).

Inlier Keypoint correspondence: