CS 6505: Supplemental Notes on Undecidability

CS 6505: Computation and Algorithms

Supplemental: Reductions and the Halting Problem

Scott McManus

When we want to show that a language is undecidable, we want to somehow rely on using the fact that the Halting Problem is undecidable. So here's how we want to show that a language L is undecidable. Suppose L is not undecidable. Then there is a decider, say D, that decides L.

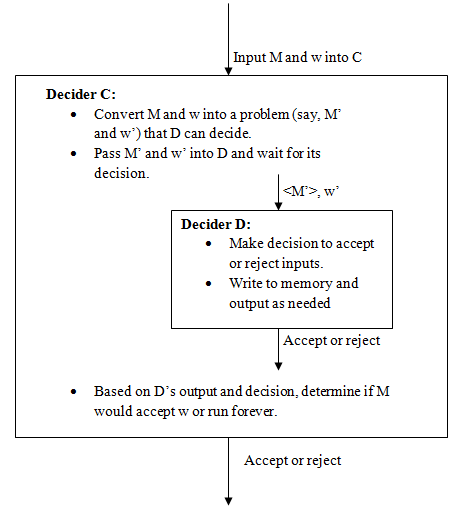
The next step is to construct another machine, say C, that takes advantage of D to somehow decide the halting problem. This relationship is shown in Figure 1 below.

Figure 1: General reduction to the halting problem

C's job is to decide the halting problem for when a Turing Machine M is run on w. C will make some modifications to M and w and pass them along to D. When D makes its decision, C can read D's output and final state of "accept" or "reject". C will now be able to say that the result of D operating on M' and w' will let it decide if M halts on w. Now we're done: If C can use D's computation results to decide if M halts on w, then C has solved the halting problem. But we know that the halting problem cannot be decided, so this result is impossible. So then such a decider D cannot exist, and the language L cannot be decided.

Example Reduction

Let's see this in action. This example is very similar to the in-class problem that we did on the first week of class. Let L = { <X>, y : Turing Machine X outputs "GT" at any point in its computation }. We want to prove that L is undecidable. Suppose not. Then there exists a decider D that, when given input machine X and input string y, will decide if X ever outputs "GT" in its computation. So now C will use D to decide the halting problem for input machine M and input string w. C does the following:

Create a new Turing Machine M' and string w' that does the following:
- In M and w, replace every occurrence of "G" with a "g". Likewise replace every occurrence of "T" with a "t".
- Simulate M on w.
- When M reaches its accept state, have it output "GT".
- When M reaches its reject state, output "reject"
Run D on M' and w'.
If D accepts M', then accept. If D rejects M', then reject.

What happens when we run C on Turing Machine M and input w? If M accepts w, then M' will print "GT". If M rejects w, then M' will never print "GT" - we substituted all of the possible "G"s and "T"s with lowercase "g" and "t". If M loops forever, M' will still not print out "GT". So we've solved the halting problem for M and w! But solving the halting problem is impossible, so D could not have decided L (i.e., D could not have decided if any Turing Machine X ever printed out "GT" when given any input y). So L is undecidable.